Mixtures of Experts
《Adaptive Mixture of Local Experts》

论文链接:https://www.cs.toronto.edu/~hinton/absps/jjnh91.pdf
1991年,由 Hinton和 Jordan提出,这是最早的MoE架构。
核心思想:通过多个独立专家网络处理输入数据不同子集,并由门控网络动态选择专家。每个专家接受相同的输入数据,但通过门控网络的动态分配,专家会专注于处理输入空间的特定区域。
基础架构
如图,一个由专家网络和门控网络组成的系统。每个专家是一个前馈网络,所有专家接收相同的输入,并具有相同数量的输出。门控网络也是一个前馈网络,通常接收与专家网络相同的输入。它的输出是归一化的 $ p_j = \exp(r_j) / \sum_i \exp(r_i) $,其中 $ r_j $是门控网络输出单元 $j$ 接收的总加权输入。选择器(selector)类似于一个多输入单输出的随机开关;开关选择来自专家 $ j $ 的输出的概率为 $p_j$ 。每个专家通常只会被分配到可能输入向量空间的一个小区域内。
系统由多个专家网络和一个门控网络组成。每个专家是一个前馈网络,处理特定子任务;门控网络根据输入决定每个专家的混合比例(概率)。
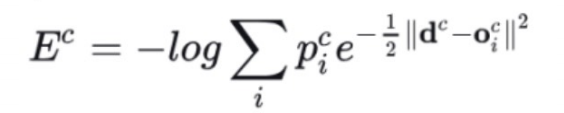
通过重新定义误差函数,鼓励专家竞争而非协作,确保每个专家专注于特定子任务。传统误差函数(如均方误差)会导致专家协作,增加耦合;论文提出优比损失(基于高斯混合模型的负对数概率),使专家独立学习,减少干扰。改进后的误差函数使门控网络倾向于选择最适合的专家,加快收敛。
性能比较
元音辨别:区分多说话者元音区分(识别元音 [i], [I], [a], [A])。
数据集:来自 75 个说话者的共振峰数据(Peterson 和 Barney, 1952),前 50 个用于训练,后 25 个用于测试。

模型能自动分解任务,专注于不同类别对(如 [i]/[I] 和 [a]/[A]),仅 2-3 个专家在最终混合中活跃。
混合专家模型达到误差标准明显快于反向传播网络,平均只需要大约一半的周期数。混合模型的学习时间也随着专家数量的增加而很好地扩展。混合专家模型具有较小但统计上显著的平均周期数优势。
总结
这篇论文针对的问题是在不同场合执行不同任务会产生干扰,导致训练速度慢和泛化性能差。MoE 的核心思想是让专家专注于适合的子任务。这意味着某些专家的利用率较低(论文中提到最终只有 2-3 个专家活跃),后续的论文大多都是在解决这个问题。
论文展示了 MoE 模型的任务分解过程:初始阶段,门控网络给所有专家分配相等的混合比例,导致每个专家处理的案例数量大致相等,决策线趋向于处理所有案例的平均最优解。随着训练进行,竞争机制使专家分化,专注于特定子任务,从而形成更符合数据分布的最优决策面。这种机制显著减少了干扰,训练速度比反向传播网络快约 50%,体现了 MoE 架构在训练时间上的优势。
《Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer》
超大型神经网络:稀疏门控混合专家层
论文链接:https://arxiv.org/abs/1701.06538
2017年,合作作者中还有Hinton和 Jordan,在LSTM层之间应用MoE卷积。仅以微小的计算效率损失就取得了超过 1000 倍的模型容量提升,并在公共语言建模和翻译数据集上显著提升了最先进的结果。
上一篇强调的是减小时间成本,这一篇是减小计算成本。

基础架构
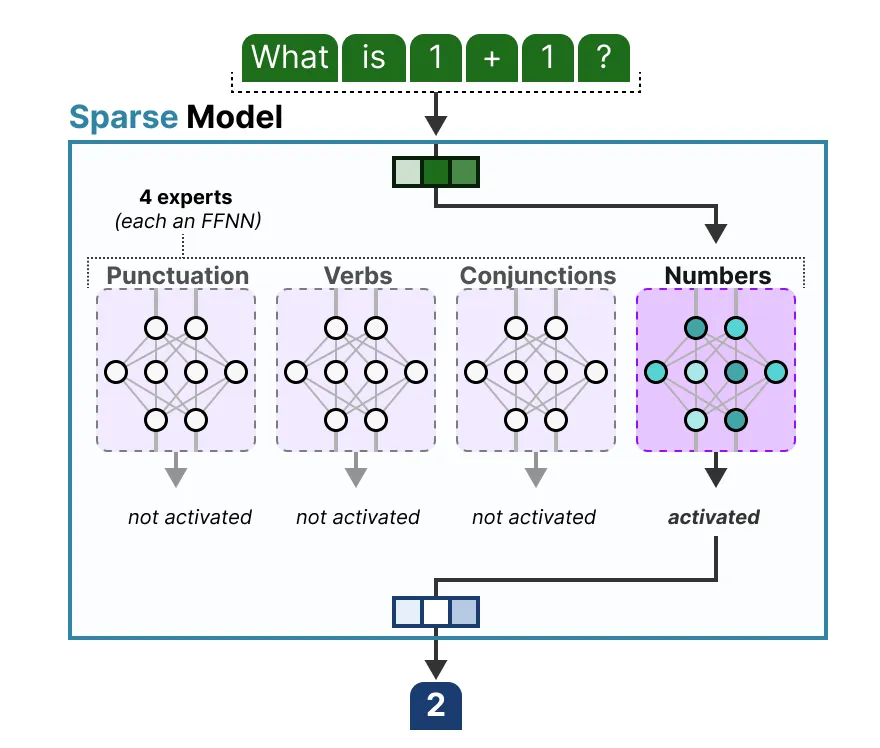
稀疏门控专家混合层(MoE)
MoE 由很多专家组成,每个专家相当于一个前馈神经网络。以及一个可训练的门控网络,该网络选择专家的稀疏组合来处理每个输入。网络的所有部分都通过反向传播进行联合训练。
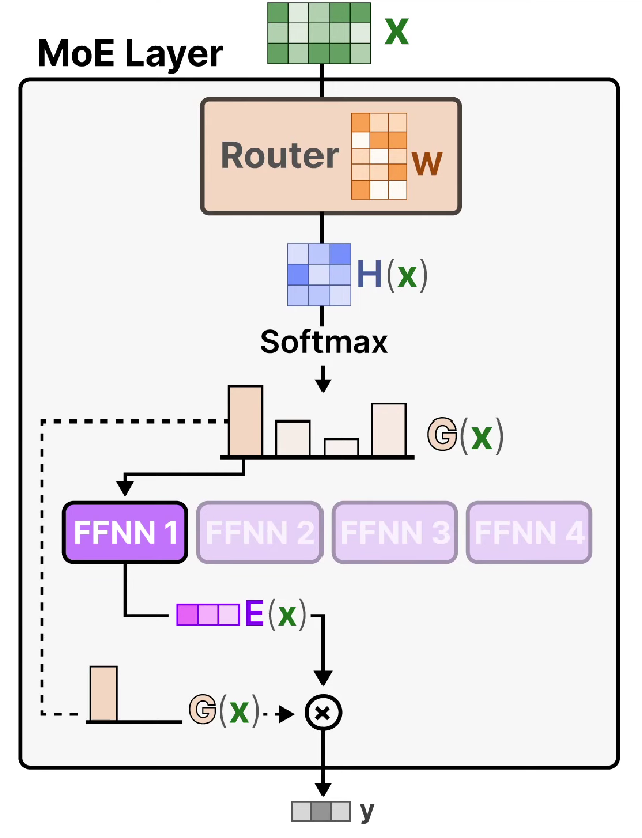
设 $ G(x) $和 $ E_i(x) $ 分别为给定输入 $ x $ 的门控网络输出和第 $ i $ 个专家网络的输出。MoE 模块的输出 $ y $ 可表示为:
$$
y = \sum_{i=1}^{n} G(x)_i E_i(x)
$$
均衡负载
门控网络总是倾向于收敛到一种状态,在这种状态下,它总是对同一批专家产生较大的权重,使得被偏好的专家训练得更快,更容易被门控网络选中。希望在训练和推理过程中,专家的重要性相等,称之为负载平衡 。某种程度上,这是为了防止对同一个专家过度拟合。
Keep Top-K
Noisy Top-K Gating
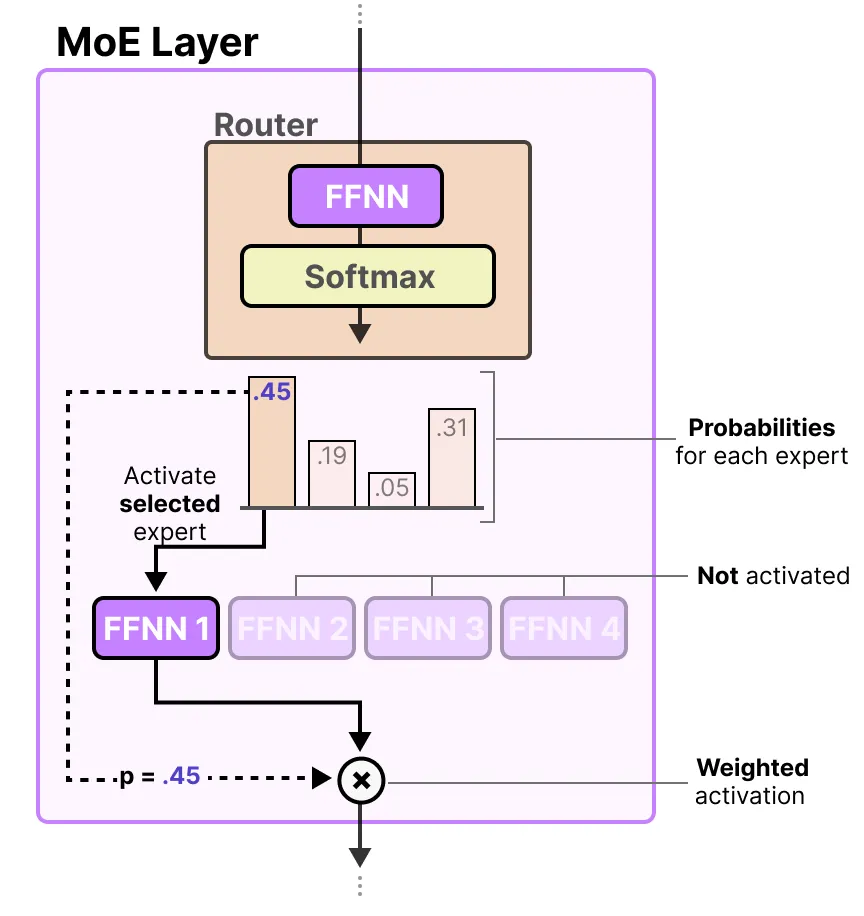
添加了两个组件:稀疏性和噪音。在应用 Softmax 函数之前,添加可调的高斯噪声,然后仅保留前 $ k $ 个值,将其余值设为 $-\infty$(这会导致对应的门控值为 0)。每部分的噪声量由可训练权重矩阵 $ W_{\text{noise}} $ 控制。通过简单的反向传播训练门控网络。稀疏性用于节省计算,噪声项有助于负载均衡。
Noise
使用Noisy Top-K Gating方法改进MoE层,引入可训练的 Gaussian 噪声防止总是选择相同的专家。
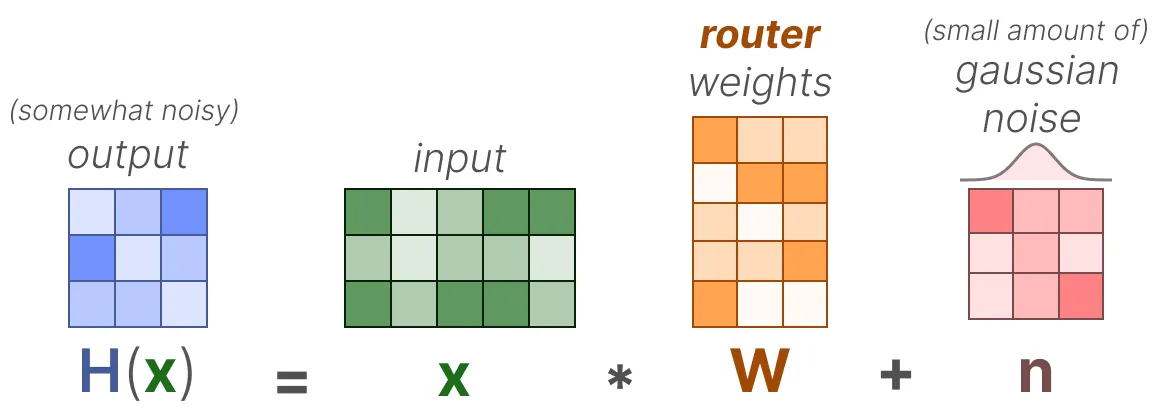 $$ H(x)_i = (x \cdot W_g)_i + \text{StandardNormal}() \cdot \text{Softplus}((x \cdot W_{\text{noise}})_i) $$
$$ H(x)_i = (x \cdot W_g)_i + \text{StandardNormal}() \cdot \text{Softplus}((x \cdot W_{\text{noise}})_i) $$Sparse
除了想要激活的前 k 名专家之外,其他所有专家的权重都将设置为 $-\infty$ 。
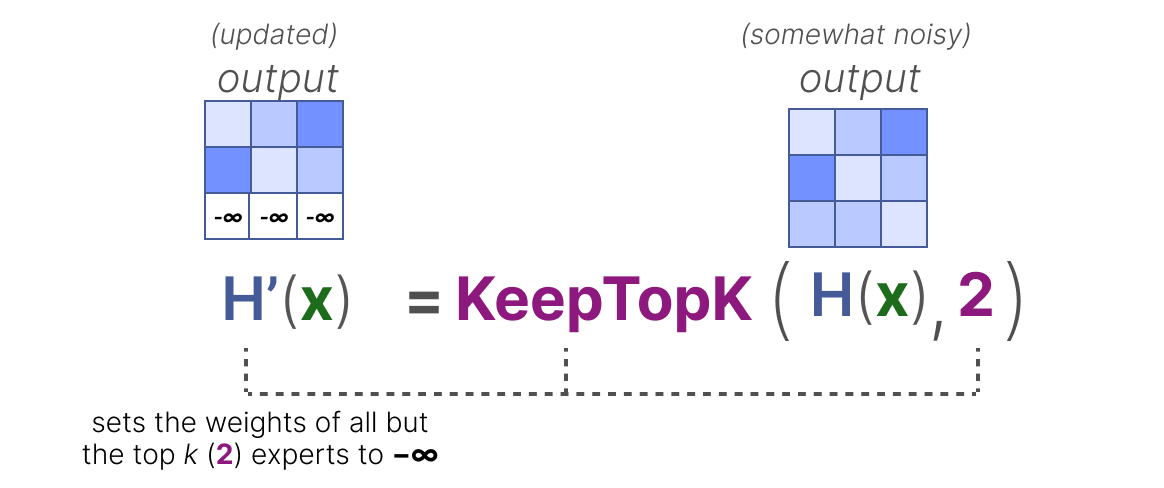 $$ \text{KeepTopK}(v, k)_i = \begin{cases} v_i & \text{if } v_i \text{ is in the top } k \text{ elements of } v, \\\ -\infty & \text{otherwise}. \end{cases} $$ 通过将这些权重设置为 $-\infty$ ,SoftMax 在这些权重上的输出将产生概率 0 :
$$ \text{KeepTopK}(v, k)_i = \begin{cases} v_i & \text{if } v_i \text{ is in the top } k \text{ elements of } v, \\\ -\infty & \text{otherwise}. \end{cases} $$ 通过将这些权重设置为 $-\infty$ ,SoftMax 在这些权重上的输出将产生概率 0 : 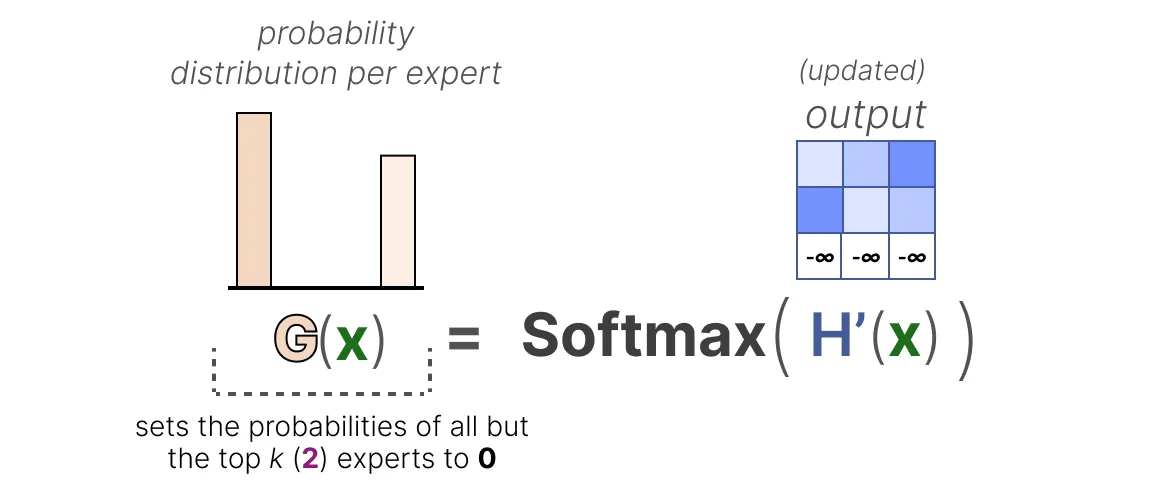 $$ G(x) = \text{Softmax}(\text{KeepTopK}(H(x), k)) $$
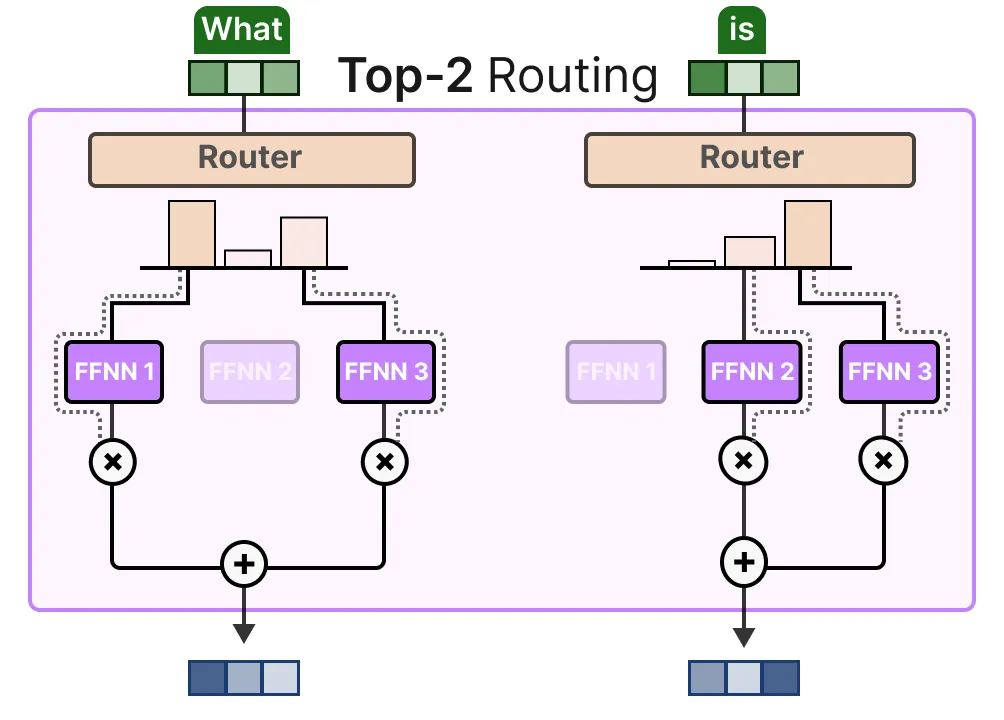
$$ G(x) = \text{Softmax}(\text{KeepTopK}(H(x), k)) $$KeepTopK 策略将每个 token 路由给几个选定的专家。
Auxiliary Loss
为了在训练过程中获得更均匀的专家分布,辅助损失(也称为负载平衡损失 )被添加到网络的常规损失中。它增加了一个约束,迫使专家具有同等重要性。
该辅助损失的第一个组成部分是将整个批次中每个专家的门控值相加。
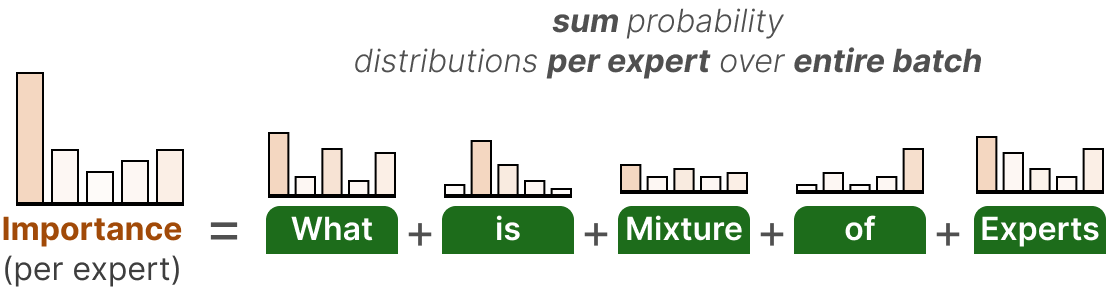 $$ \text{Importance}(X) = \sum_{x \in X} G(x) $$ 这为我们提供了每个专家的重要性分数 ,该分数表示无论输入如何,选择特定专家的可能性。可以用它来计算变异系数 ( CV ),它告诉我们专家之间重要性得分的差异有多大。利用这个 CV 分数,我们可以在训练期间更新辅助损失 ,以尽可能降低 CV 分数( 从而给予每个专家同等的重要性 )。
$$ \text{Importance}(X) = \sum_{x \in X} G(x) $$ 这为我们提供了每个专家的重要性分数 ,该分数表示无论输入如何,选择特定专家的可能性。可以用它来计算变异系数 ( CV ),它告诉我们专家之间重要性得分的差异有多大。利用这个 CV 分数,我们可以在训练期间更新辅助损失 ,以尽可能降低 CV 分数( 从而给予每个专家同等的重要性 )。 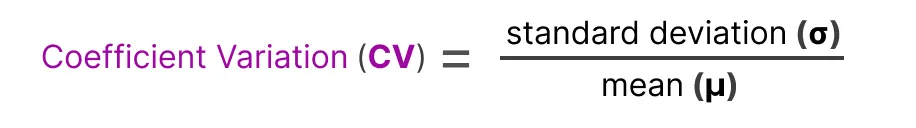
如果重要性分数存在很大差异,则 CV 会很高,相反,如果所有专家的重要性得分都相似,那么 CV 就会较低
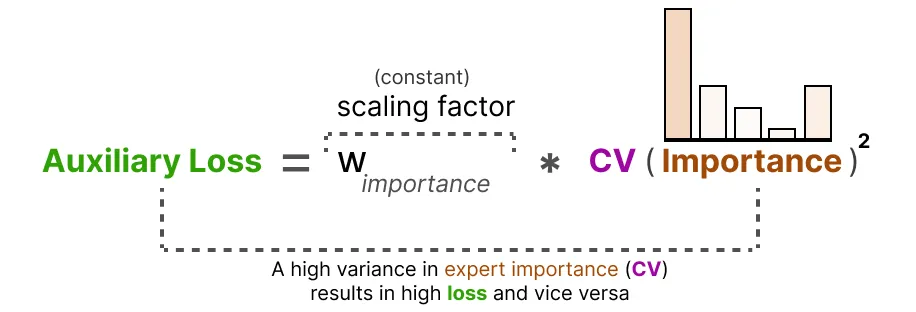 $$ L_{\text{importance}}(X) = w_{\text{importance}} \cdot CV(\text{Importance}(X))^2 $$ 最后,将辅助损失作为单独的损失添加,以便在训练期间进行优化。
$$ L_{\text{importance}}(X) = w_{\text{importance}} \cdot CV(\text{Importance}(X))^2 $$ 最后,将辅助损失作为单独的损失添加,以便在训练期间进行优化。虽然这种损失函数可以确保平衡的重要性,但专家仍然可能收到数量非常不同的样本。为了解决这一问题,论文引入了 $ L_{\text{load}} $ 损失,专门用于平衡专家接收的样本数量(即负载均衡),与 $ L_{\text{importance}} $ 损失(平衡门控权重总和)配合使用。
Load-Balancing Loss
专家接收的样本数量是一个离散值,无法用于反向传播。所以这里定义了一个平滑估计器 $Load(X)$,用于估计每个专家在输入批次 $X$ 中分配到的示例数量,通过概率计算来近似样本分配。平滑性使得可以通过估计器反向传播梯度。这是门控函数中噪声项的目的。
对于一个输入批次 $ X $,第 $ i $ 个专家的负载定义为:
$$ {Load}(X)_i = \sum_{x \in X} P(x, i) $$
其中 $ P(x, i) $ 是给定输入 $ x $ 时第 $ i $ 个专家被选中的概率,它描述了第 $ i$ 个专家的“带噪声得分”大于某个阈值的概率。论文通过噪声 Top-K 门控的特性计算 $ P(x, i) $:
$$ P(x, i) = \Pr\left( (x \cdot W_g)_i + \text{StandardNormal}() \cdot \text{Softplus}((x \cdot W_{\text{noise}})_i) > k{th\_excluding}(H(x), k, i) \right) $$
$ (x \cdot W_g)_i $:
- $x $ 是输入向量(例如来自上一层的 LSTM 输出)。
- $ W_g $ 是门控网络的可训练权重矩阵。
- $ (x \cdot W_g)_i $ 是第 $ i $ 个专家的原始得分(未添加噪声),表示门控网络对第 $ i $ 个专家的“偏好”。
$ StandardNormal()⋅Softplus((x⋅Wnoise)i) $:
- $ \text{StandardNormal}() $:表示从均值为 0、标准差为 1 的标准正态分布中采样一个随机数。
- $ (x \cdot W_{\text{noise}})_i $:通过另一个可训练权重矩阵$ W_{\text{noise}} $ 计算的噪声控制项。
- $ \text{Softplus}((x \cdot W_{\text{noise}})_i) $:这部分计算噪声的标准差。它通过将输入 $x$ 与另一个可训练的权重矩阵 $W_{noise}$ 相乘,然后应用 Softplus 函数 $ \text{Softplus}(z) = \log(1 + e^z) $ 来确保标准差为正值。这个标准差是可调节的,并且依赖于输入 $x$ 。
- 这部分是加到原始得分上的高斯噪声,表示一个高斯噪声项,均值为 0,方差由 $ \text{Softplus}((x \cdot W_{\text{noise}})_i) $决定。噪声的引入有助于负载均衡,避免门控网络总是选择固定的专家。
$$ H(x)_ i = (x \cdot W_g)_i + \text{StandardNormal}() \cdot \text{Softplus}((x \cdot W_{\text{noise}})_i $$
$H(x)_i$代表了第$ i $个专家的最终“带噪声得分”。
$k\text{th_excluding}(H(x), k, i)$: 这是决定专家 i 是否被选中的阈值。它的含义是:在向量 $H(x)$(包含了所有专家的带噪声得分)中,排除掉第 i 个专家自身的分数后,找到剩下 n−1 个分数中第 k 大的分数 。
$Pr(⋯>…): $ 公式计算 $ H(x)_ i $(重新采样噪声后)大于 $k\text{th_excluding}(H(x), k, i)$ 的概率。在噪声 Top-K 门控中,第 $𝑖$ 个专家被选中当且仅当 $ H(x)_ i$ 是 $𝐻 ( 𝑥 )$ 中前 $𝑘$ 大的值。
$$ P(x, i) = \Phi\left( \frac{(x \cdot W_g)_i - k{th\_ excluding}(H(x), k, i)}{\text{Softplus}((x \cdot W_{\text{noise}})_i)} \right) $$
Φ 表示标准正态分布的累积分布函数(CDF)。利用正态分布的 CDF 给出了计算这个概率的具体数学表达式,方便进行计算和反向传播(因为 Φ 是可微的)。这整个机制是为了在选择专家时引入随机性(有助于负载均衡 )并估算每个专家被选中的概率,进而定义$L_{load}$损失。
$$ L_{\text{load}}(X) = w_{\text{load}} \cdot CV(\text{Load}(X))^2 $$
初始负载不平衡:为了避免内存溢出错误,需要在近似相等的专家负载状态下初始化网络(因为软约束需要一些时间才能发挥作用)。为了实现这一点,将矩阵 $W_g$ 和 $W_{noise}$ 初始化为全零,这样就不会产生信号,而只有一些噪声。
Hierarchical Mixture-of-Experts
层次 MoE 是一种分层结构的 MoE,如果专家数量非常庞大,可以使用两层分层MoE来降低分支因子。在一个分层MoE中,一个主门控网络选择一个稀疏加权组合的“专家”,每个“专家”本身就是一个具有自己门控网络的二级混合专家。
第一级(主门控网络):主门控网络 $ G_{\text{primary}} $ 负责选择一组“专家组”(groups of experts)。
第二级(次级门控网络):每个专家组内有一个次级门控网络 $G_i $,负责在该组内选择具体的专家。
专家网络:最终的专家网络 $E_{i,j} $,其中 $ i $ 表示组索引,$j $ 表示组内的专家索引。
$$ y_H = \sum_{i=1}^{a} \sum_{j=1}^{b} G_{\text{primary}}(x)_i \cdot G_i(x)_j \cdot E_{i,j}(x) $$
$Gprimary(x)i$:主门控网络对第 $ i $ 个组的权重。
$G_i(x)_j $:第 $ i $ 个组的次级门控网络对组内第 $j $ 个专家的权重。
$ E_{i,j}(x) $:第 $ i $ 个组中第 $j $ 个专家的输出。
对专家利用率的衡量指标将更改为以下内容:
$$ \text{Importance}_H(X)_{i,j} = \sum_{x \in X} G_{\text{primary}}(x)_i \cdot G_i(x)_j $$
$$ \text{Load}_H(X)_{i,j} = \frac{\text{Load}_{\text{primary}}(X)_i \cdot \text{Load}_i(X^{(i)})_j}{|X^{(i)}|} $$
$Load_{primary}$ 和 $Load_i$ 分别表示主门控网络和 $i^{th}$ 次级门控网络的加载函数。 $ X^{(i)}$表示 X 中满足 $ G_{primary}(x)_i > 0 $ 的子集。
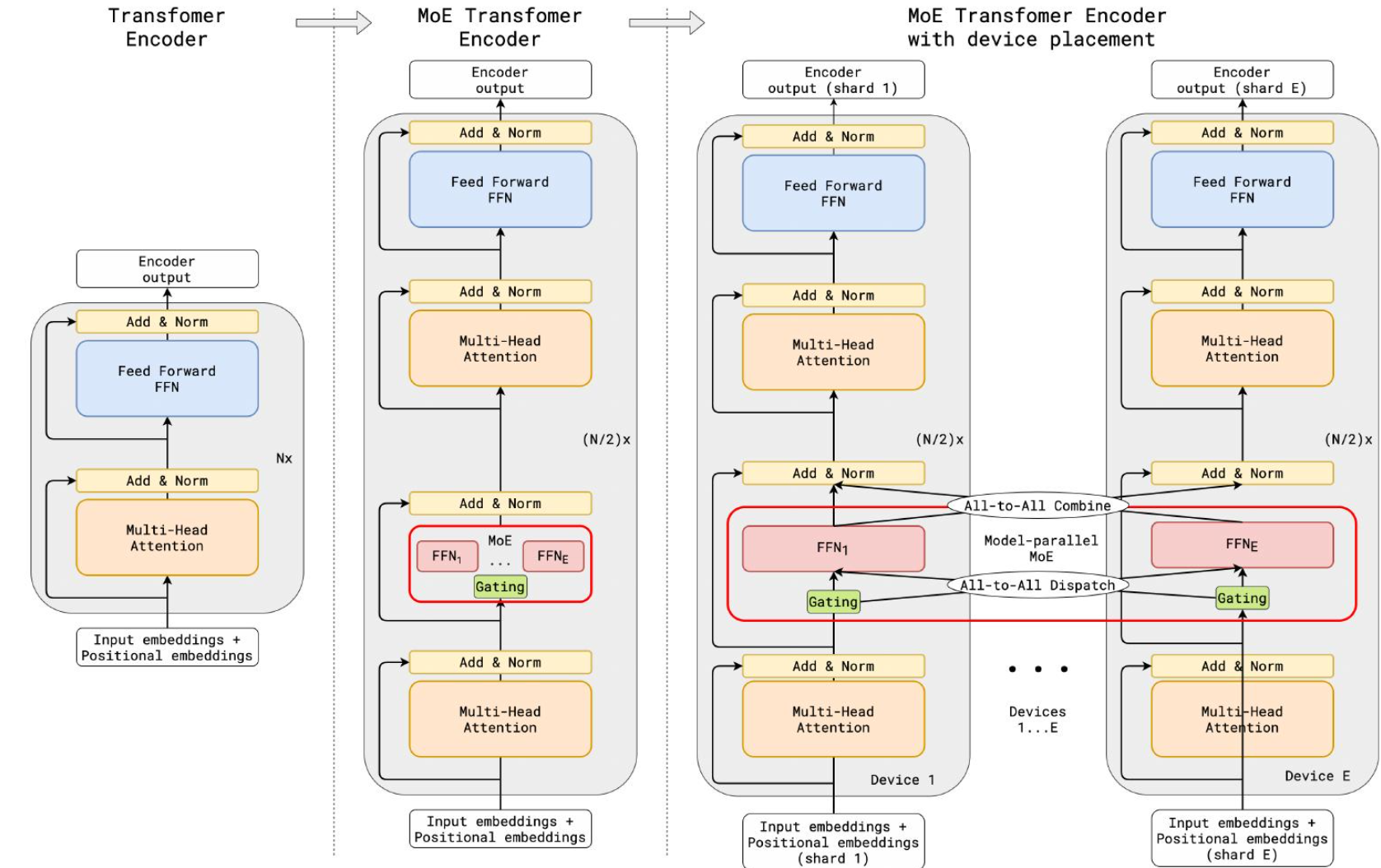
《GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding》
基于条件计算和自动分片的巨型模型扩展。
论文链接:https://arxiv.org/abs/2006.16668
创新点
Expert Capacity
专家容量
不平衡不仅存在于所选专家中,还存在于发送给专家的token分配中。如果输入 token 不成比例地发送给一个专家而不是另一个专家,那么也可能导致训练不足。
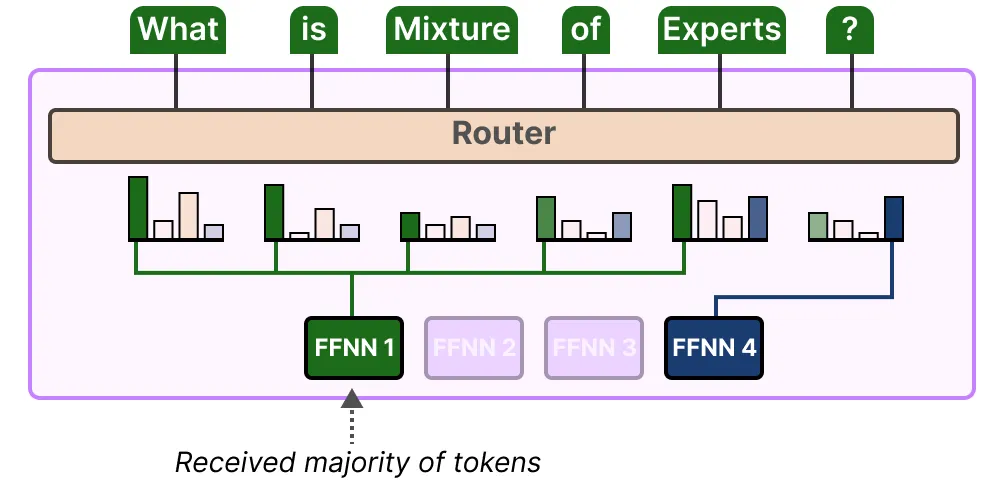
解决这个问题的一个方法是限制每个专家可以处理的 token 数量,即专家容量 。当专家达到容量上限时,产生的 token 将被发送给下一个专家:
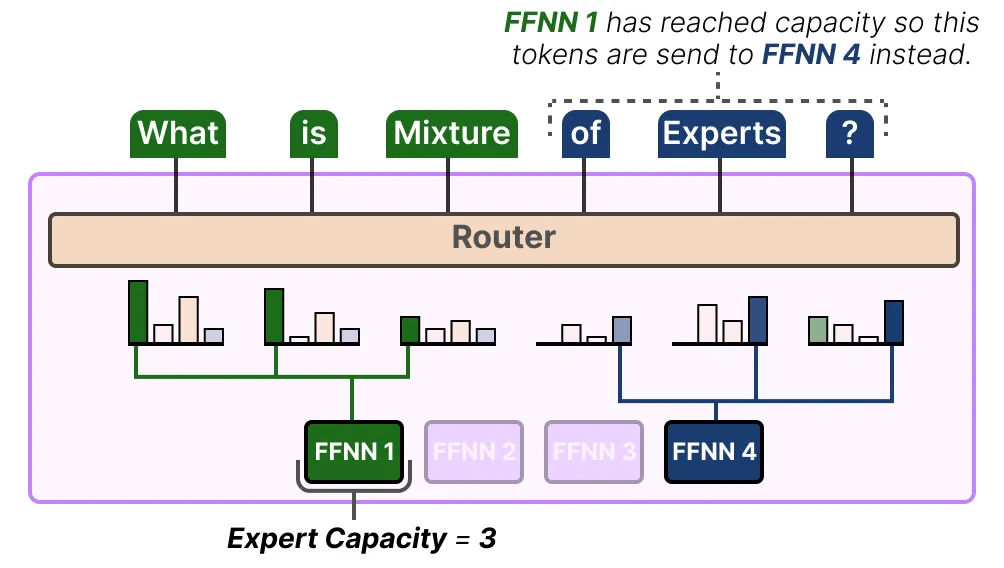
如果两个专家都已达到其容量上限,则 token 将不会被任何专家处理,而是被发送到下一层。这称为 token 溢出 。这些token的表示通过残差连接传递到下一层。

Auxiliary loss
门控函数不应总是选择相同的一小部分专家,因为这会导致一小部分专家容量溢出,而其余专家则被闲置。定义了一个辅助损失项 ℓaux 来强制执行此约束。 它被添加到模型的总损失函数中 L = ℓnll + k ∗ ℓaux,其中 k 是一个常数乘数。
Random routing
随机路由机制
在 top-2 设计中,始终选择表现最优的专家,但第二选择的专家则根据其权重以一定概率被选中。
《Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity》
论文链接:https://arxiv.org/abs/2101.03961
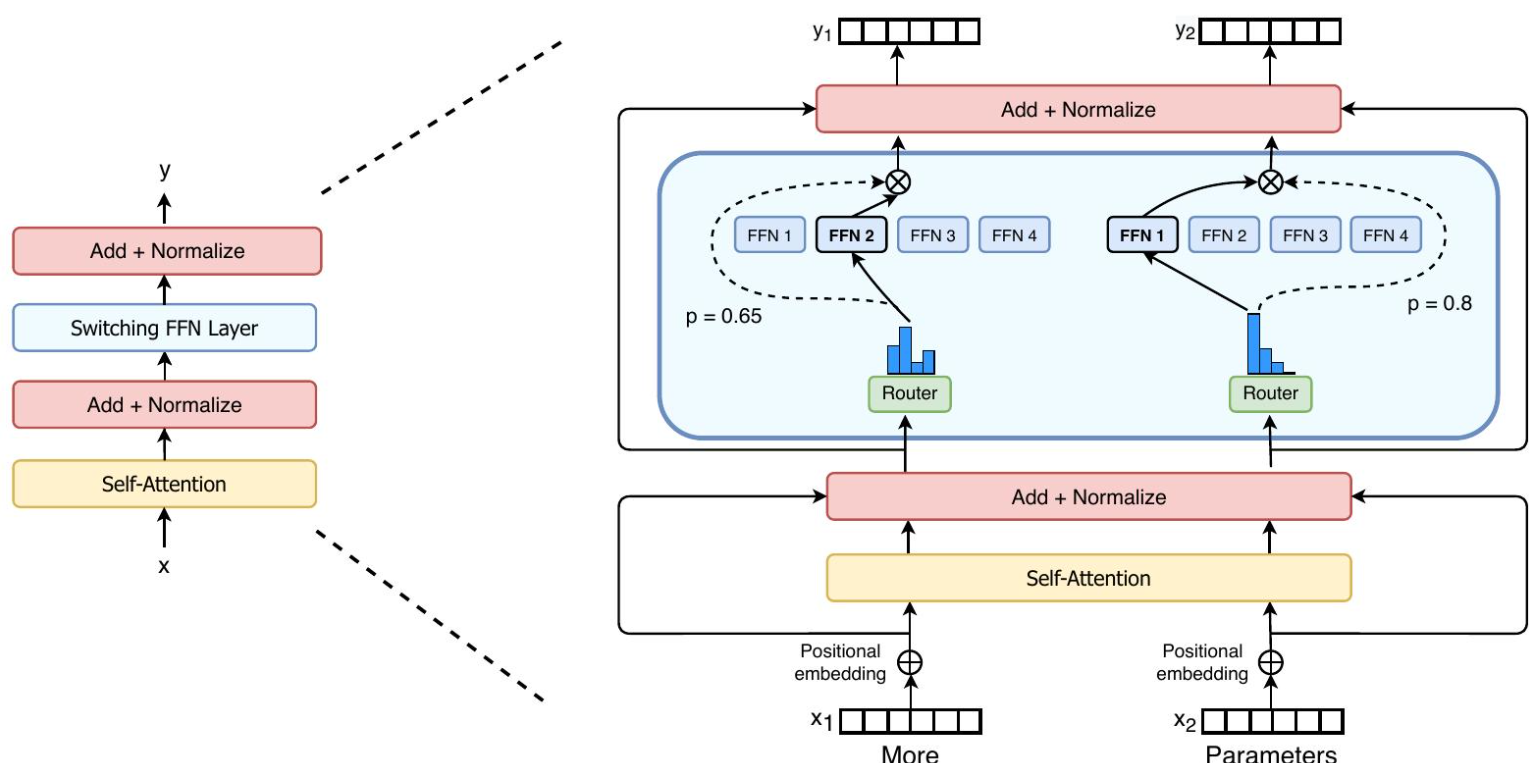
简化了MoE路由算法,并设计了直观的改进模型,从而降低了通信和计算成本。提出的训练技术减轻了不稳定性,并且证明了可以使用较低精度(bfloat16)格式首次训练大型稀疏模型。将 Switch 层添加到 Transformer 的自注意力层中。
Switch Routing
(1)仅将token路由到单个专家,因此减少了路由器计算。
(2)由于每个token仅被路由到单个专家,因此每个专家的批次大小(专家容量)可以至少减半。
(3)路由实现得到简化,并且通信成本降低。
《DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models》
现有MoE架构问题
(1)知识混合性:现有的MoE实践通常采用数量有限的专家(例如,8个或16个),因此分配给特定专家的token可能涵盖各种知识。因此,指定的专家将倾向于在其参数中组合截然不同的知识类型,而这些知识很难同时利用。
(2)知识冗余:分配给不同专家的token可能需要共同的知识。因此,多个专家可能会收敛于在其各自的参数中获取共享知识,从而导致专家参数的冗余。
这些问题共同阻碍了现有MoE实践中的专家专业化,使其无法达到MoE模型的理论性能上限。
我个人感觉第一个问题和第一篇论文提出的目的应该是一致的,一个模型在不同场合执行不同任务会产生干扰,然后这里的专家又出现了这个问题,使得专家的专业化程度较低。
解决问题的主要策略
(1)细粒度专家分割:在保持参数数量不变的同时,我们通过分割 FFN 中间隐藏维度将专家分割成更细的粒度。相应地,在保持恒定计算成本的同时,我们也激活更多细粒度的专家,以实现激活专家的更灵活和适应性更强的组合。细粒度的专家分割使得不同的知识能够被更精细地分解,并被更精确地学习到不同的专家中,其中每个专家将保持更高的专业化水平。此外,激活专家组合的灵活性增加也有助于更准确和有针对性的知识获取。
(2)共享专家隔离:我们隔离某些专家作为始终激活的共享专家,旨在捕获和巩固不同上下文中的通用知识。通过将通用知识压缩到这些共享专家中,其他路由专家之间的冗余将被减轻。这可以提高参数效率,并确保每个路由专家通过专注于独特的方面来保持专业性。
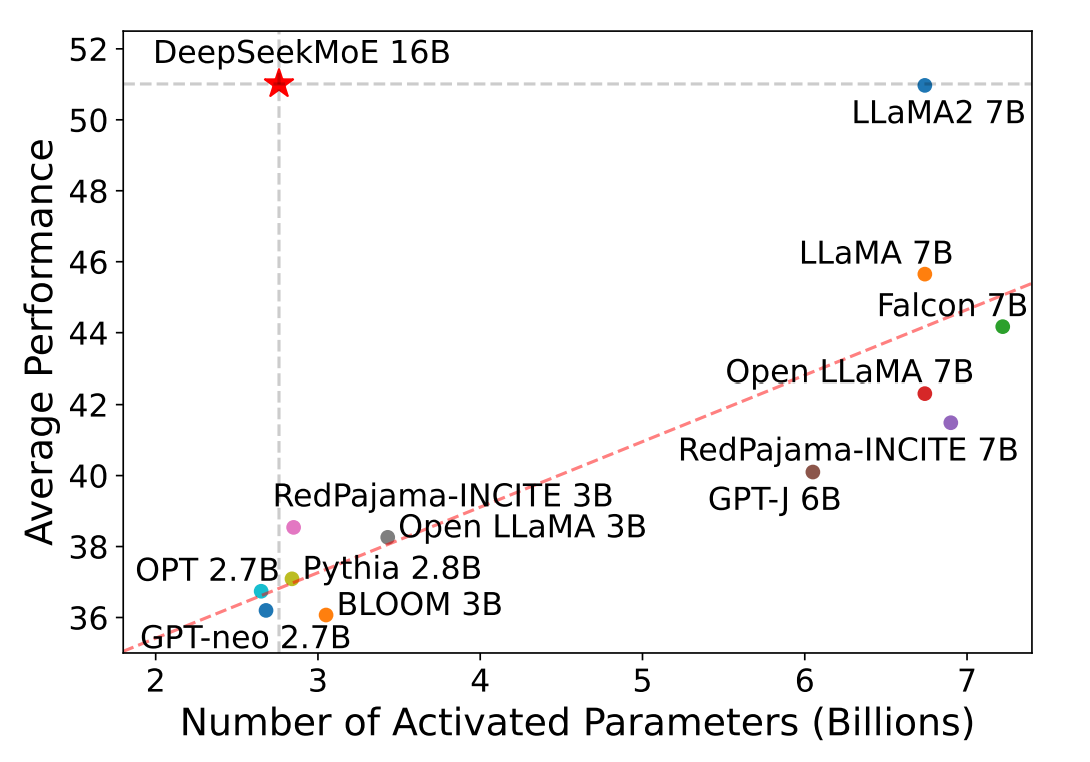
DeepSeekMoE 中的这些架构创新为训练参数高效的 MoE 语言模型提供了机会,其中每个专家都高度专业化。
DeepSeekMoE 的示意图。子图 (a) 展示了具有传统 top-2 路由策略的 MoE 层。子图 (b) 说明了细粒度专家分割策略。子图 © 展示了共享专家隔离策略的集成,构成了完整的 DeepSeekMoE 架构。值得注意的是,在这三种架构中,专家参数的数量和计算成本保持不变。
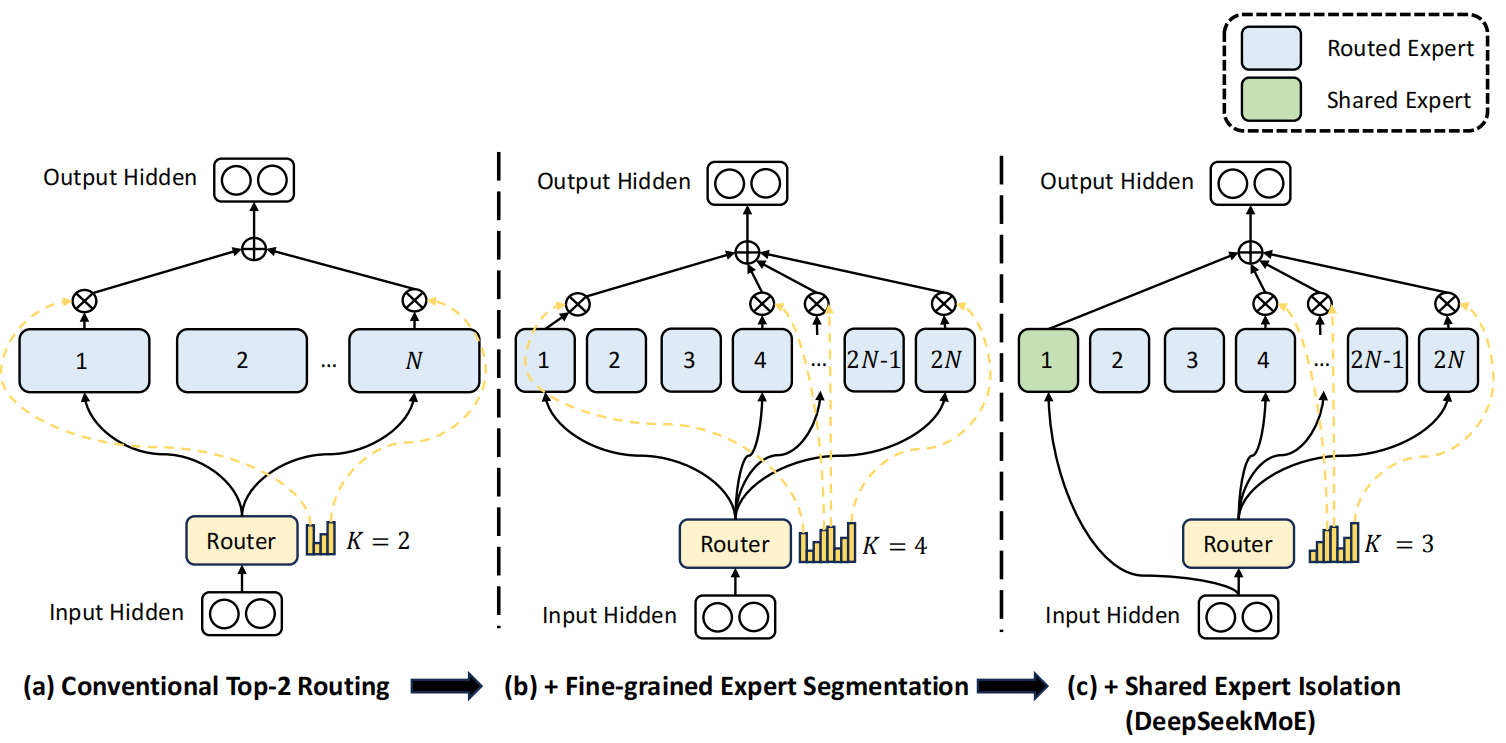
DeepSeekMoE 架构
细粒度专家分割
通过将FFN中间隐藏维度降低到原始大小的𝑚分之一,将每个专家FFN分割成𝑚个更小的专家。由于每个专家变得更小,作为回应,还将激活专家的数量增加到𝑚倍,以保持相同的计算成本。通过细粒度的专家分割,MoE层的输出可以表示为:
$$ \mathbf{h}_t^l = \sum_{i=1}^{mN} (g_{i,t} \cdot \text{FFN}_i(\mathbf{u}_t^l)) + \mathbf{u}_t^l $$
$$
g_{i,t} = \begin{cases}
s_{i,t}, & s_{i,t} \in \text{Topk}({s_{j,t}} \mid 1 \leq j \leq mN), mK), \
0, & \text{otherwise}
\end{cases}
$$
$$
s_{i,t} = \text{Softmax}_i(\mathbf{u}_t^{l^T} \mathbf{e}_i^l)
$$
其中,专家参数的总数等于 𝑁 乘以标准 FFN 中的参数数量,mN 表示细粒度专家的总数。采用细粒度专家分割策略后,非零门控的数量也将增加到 mK。
组合灵活性的激增增强了实现更准确和更有针对性的知识获取的潜力。
共享专家隔离
采用传统的路由策略,分配给不同专家的令牌可能需要一些共同的知识或信息。因此,多个专家可能会趋同于在其各自的参数中获取共享知识,从而导致专家参数的冗余。然而,如果存在专门用于捕获和整合不同上下文中的共同知识的共享专家,则可以减轻其他路由专家之间的参数冗余。这种冗余的减轻将有助于构建一个参数效率更高、专家更专业的模型。
隔离𝐾𝑠个专家作为共享专家。无论路由器模块如何,每个token都将被确定性地分配给这些共享专家。为了保持恒定的计算成本,其他路由专家中激活的专家数量将减少𝐾𝑠。通过集成共享专家隔离策略,完整DeepSeekMoE架构中的MoE层可以表述如下:
$$ \mathbf{h}_t^l = \sum_{i=1}^{K_s} \text{FFN}_i(\mathbf{u}_t^l) + \sum_{i=K_s+1}^{mN} (g_{i,t} \cdot \text{FFN}_i(\mathbf{u}_t^l)) + \mathbf{u}_t^l $$
$$
g_{i,t} = \begin{cases}
s_{i,t}, & s_{i,t} \in \text{Topk}({s_{j,t} \mid K_s + 1 \leq j \leq mN }), mK - K_s), \
0, & \text{otherwise}
\end{cases}
$$
$$
s_{i,t} = \text{Softmax}_i(\mathbf{u}_t^{l^T} \mathbf{e}_i)
$$
最后,在 DeepSeekMoE 中,共享专家的数量为 𝐾𝑠,路由专家的总数为 𝑚𝑁 − 𝐾𝑠,非零门的数量为 𝑚𝐾 − 𝐾𝑠。
负载均衡问题
自动学习的路由策略可能会遇到负载不均衡的问题,这表现出两个显著的缺陷。首先,存在路由崩溃的风险,即模型总是只选择少数几个专家,导致其他专家无法得到充分的训练。其次,如果专家分布在多个设备上,负载不均衡会加剧计算瓶颈。
Expert-Level Balance Loss
专家级平衡损失。为了降低路由崩溃的风险,平衡损失的计算如下:
$$ \mathcal{L}_{\text{ExpBal}} = \alpha_1 \sum_{i=1}^{N'} f_i p_i $$
$$
f_i = \frac{N’}{K’ T} \sum_{t=1}^{T} \mathbb{1}(\text{Token } t \text{ selects Expert } i)
$$
$$
p_i = \frac{1}{T} \sum_{t=1}^{T} s_{i,t}
$$
其中𝛼1是一个被称为专家级别平衡因子的超参数,为了简洁起见,𝑁′等于(𝑚𝑁 − 𝐾𝑠),𝐾′等于(𝑚𝐾 − 𝐾𝑠)。1(·)表示指示函数。
Device-Level Balance Loss
将所有路由的专家划分为 𝐷 组 {E1, E2, . . ., E𝐷},并将每组部署在单个设备上,则设备级别平衡损失的计算方式如下:
$$ \mathcal{L}_{\text{DevBal}} = \alpha_2 \sum_{i=1}^{D} f'_i p'_i $$
$$ f'_i = \frac{1}{|\mathcal{E}_i|} \sum_{j \in \mathcal{E}_i} f_j $$
$$ p'_i = \sum_{j \in \mathcal{E}_i} p_j $$
其中𝛼2是一个被称为设备级别平衡因子的超参数。设置一个较小的专家级别平衡因子以降低路由崩溃的风险,同时设置一个较大的设备级别平衡因子以促进设备间的均衡计算。