Unsupervised Feature Learning via Non-Parametric Instance Discrimination

论文地址：https://arxiv.org/pdf/1805.01978

代码地址：https://github.com/zhirongw/lemniscate.pytorch

引言

实例判别（Instance Discrimination） 是2018年提出的一种无监督特征学习方法，它将对比学习的思想推向极致：将每个图像实例视为一个独立的类别，通过区分不同实例来学习特征表示。这篇论文是MoCo、SimCLR等现代对比学习方法的重要先驱工作。

论文的核心洞察来自对监督学习的观察：在ImageNet上训练的神经网络，即使没有显式指导，也能自动发现视觉上相似的类别（如leopard和jaguar）之间的关联。作者将这一观察延伸到实例级别：如果能够区分每个实例，那么学习到的特征应该能够捕获实例间的视觉相似性。

实例判别的核心创新

将无监督问题转化为监督问题：

实例判别的天才之处在于一个简单的转换：

传统无监督学习：没有标签，难以定义学习目标
实例判别：每个图像就是自己的标签，变成N分类问题
好处：可以直接使用成熟的分类框架和技术

为什么这种方法有效？

视觉相似性的自然涌现
- 虽然每个实例是独立类别，但视觉相似的实例会在特征空间聚集
- 原因：它们共享底层视觉模式（边缘、纹理、形状等）
- 结果：学到的特征捕获了语义信息
信息论的解释
- 区分N个实例需要log(N)比特信息
- 模型被迫学习最有效的编码
- 这种编码自然对应于语义特征
避免平凡解
- 不能简单记住每个实例（泛化要求）
- 必须学习可迁移的特征
- 数据增强强制学习不变性

技术挑战与解决方案

挑战1：计算Softmax的分母

当有百万级实例时，计算softmax分母需要遍历所有实例，计算成本巨大。

解决方案：NCE近似

1 2	原始softmax概率：P(i\|v) = exp(v·f_i) / Σ_j exp(v·f_j) NCE近似：将其转化为二分类问题（实例i vs 噪声）

挑战2：存储所有实例的特征

需要存储所有训练图像的特征表示，内存需求大。

解决方案：Memory Bank

使用动量更新：新特征 = m×旧特征 + (1-m)×当前特征
好处：平滑特征变化，提高训练稳定性
内存需求：128维×100万实例 ≈ 500MB（可接受）

挑战3：负样本采样

从百万实例中采样负样本，如何保证采样质量？

解决方案：Proximal Regularization

不是随机采样，而是基于特征相似度
优先采样相似但不同的实例（困难负样本）
提高学习效率

核心思想

基本动机

关键观察：

监督学习中，模型会自动学习到视觉相似类别之间的关联
这种相似性不是来自语义标注，而是来自视觉数据本身
如果将类别级别的监督推向实例级别，能否学到更好的表示？

核心假设：

每个图像实例本身就是一个独特的"类别"
通过区分不同实例，模型会学习到捕获视觉相似性的特征
视觉相似的实例在特征空间中应该更接近

方法概述

将无监督学习问题转化为实例级别的分类问题：

每个训练图像是一个独立的类别
使用非参数softmax进行分类
使用NCE（Noise-Contrastive Estimation）解决计算问题

方法详解

非参数Softmax分类器

参数化Softmax的问题

传统的参数化softmax：
$$
P(i|v) = \frac{\exp(w_i^T v)}{\sum_{j=1}^{n} \exp(w_j^T v)}
$$

其中 $w_j$ 是类别 $j$ 的权重向量。

问题：

权重向量 $w_j$ 只对训练类别有效，无法泛化到新实例
权重向量作为类别原型，阻止了实例间的直接比较
需要存储和更新大量权重参数

非参数Softmax

将权重向量 $w_j$ 替换为特征向量 $v_j$：
$$
P(i|v) = \frac{\exp(v_i^T v / \tau)}{\sum_{j=1}^{n} \exp(v_j^T v / \tau)}
$$

其中：

$v_i, v_j$ 是归一化后的特征向量（$||v|| = 1$）
$\tau$ 是温度参数，控制分布的尖锐程度

优势：

直接比较实例：特征向量直接作为"类别原型"
泛化能力强：学习到的特征可以应用到任何新实例
计算高效：无需存储和更新权重参数
训练测试一致：训练和测试都使用相同的度量空间

Memory Bank机制

问题：计算 $P(i|v)$ 需要所有实例的特征 ${v_j}$，但每次迭代只更新当前batch的特征。

解决方案：维护一个Memory Bank $V = {v_j}$ 存储所有实例的特征。

更新策略：

初始化：Memory Bank中的特征初始化为随机单位向量
更新：每次迭代后，将当前batch的特征更新到Memory Bank
使用：计算损失时，从Memory Bank中读取特征

优势：

避免每次重新计算所有特征
保持特征的历史信息
计算效率高

Noise-Contrastive Estimation (NCE)

问题：当实例数量 $n$ 很大（如ImageNet的1.2M）时，计算完整的softmax不可行。

解决方案：使用NCE将多类分类问题转化为二分类问题。

NCE原理

将问题转化为：区分数据样本和噪声样本。

定义：

数据分布：$P_d(i\mid v) = \frac{\exp(v_i^\top v / \tau)}{Z_i}$，其中 $Z_i = \sum_{j=1}^{n} \exp(v_j^\top v / \tau)$
噪声分布：$P_n(i) = 1/n$（均匀分布）
噪声样本频率：$m$ 倍于数据样本

后验概率：

$$ h(i, v) = P(D=1\mid i, v) = \frac{P_d(i\mid v)}{P_d(i\mid v) + m \cdot P_n(i)} $$

损失函数：

$$ \mathcal{L}_{\text{NCE}}(\theta) = -\mathbb{E}_{(i,v)\sim P_d}[\log h(i, v)] - m \cdot \mathbb{E}_{(i,v')\sim P_n}[\log\big(1 - h(i, v')\big)] $$

归一化常数估计

计算 $Z_i$ 仍然昂贵，使用蒙特卡洛估计：

$$ Z_i \approx \frac{n}{m} \sum_{k=1}^{m} \exp\big(v_{j_k}^\top v / \tau\big) $$
其中 ${j_k}$ 是随机采样的索引。

复杂度：从 $O(n)$ 降低到 $O(1)$ 每个样本。

Proximal Regularization（近端正则化）

问题：每个"类别"只有一个实例，每个epoch每个类别只访问一次，训练过程振荡严重。

解决方案：引入近端正则化项，鼓励训练过程的平滑性。

正则化项：

$$ \lambda \big\lVert v_i^{(t)} - v_i^{(t-1)} \big\rVert_2^2 $$

其中：

$v_i^{(t)}$ 是当前迭代的特征
$v_i^{(t-1)}$ 是Memory Bank中存储的特征（上一迭代）

完整损失：

$$ \mathcal{L}_{\text{NCE}}(\theta) = -\mathbb{E}_{(i,v)\sim P_d}\Big[\log h\big(i, v_i^{(t-1)}\big) - \lambda \big\lVert v_i^{(t)} - v_i^{(t-1)} \big\rVert_2^2\Big] - m \cdot \mathbb{E}_{(i,v')\sim P_n}\Big[\log\big(1 - h(i, v'^{(t-1)})\big)\Big] $$

加权k-NN分类器

测试时分类：

计算特征：$\hat{f} = f_\theta(\hat{x})$
相似度计算：$s_i = \cos(v_i, \hat{f})$
k-NN检索：找到top-k最近邻 $N_k$
加权投票：类别 $c$ 的权重为
$$
w_c = \sum_{i \in N_k} \alpha_i \cdot \mathbf{1}(c_i = c)
$$
其中 $\alpha_i = \exp(s_i / \tau)$

参数设置：

$k = 200$
$\tau = 0.07$（与训练时相同）

实验分析

参数化 vs 非参数化Softmax

在CIFAR-10上的对比实验：

方法	Linear SVM	k-NN
参数化Softmax	60.3%	63.0%
非参数化Softmax	75.4%	80.8%

关键发现：

非参数化方法显著优于参数化方法（+18%）
k-NN性能接近线性SVM，说明学习到的特征度量质量高

NCE近似质量

不同负样本数量 $m$ 的影响：

m	k-NN Accuracy
1	42.5%
10	63.4%
512	78.4%
4096	80.4%

结论：随着 $m$ 增加，NCE近似质量提升，$m=4096$ 时接近完整softmax。

ImageNet分类结果

不同网络架构的性能：

方法	conv5 (Linear)	k-NN	特征维度
Random	14.1%	3.5%	10K
Split-Brain	35.2%	11.8%	10K
Ours (AlexNet)	35.6%	31.3%	128
Ours (VGG16)	39.2%	33.9%	128
Ours (ResNet-18)	44.5%	41.0%	128
Ours (ResNet-50)	54.0%	46.5%	128

关键发现：

显著超越SOTA：在ImageNet上大幅超越之前的方法
网络深度优势：从AlexNet到ResNet-50，性能持续提升
紧凑表示：仅用128维特征就达到优异性能
存储高效：1.28M图像的特征仅需600MB存储

特征泛化能力

在Places数据集上的零样本评估（使用ImageNet训练的特征）：

方法	ResNet-50 (conv5)	ResNet-50 (k-NN)
Ours	45.5%	41.6%

结论：学习到的特征具有良好的跨数据集泛化能力。

训练目标与测试目标的一致性

关键观察：

训练损失持续下降
测试准确率同步提升
无过拟合迹象

意义：说明训练目标（实例判别）与测试目标（语义分类）是一致的，学习到的特征确实捕获了视觉相似性。

消融实验

特征维度：

维度	Top-1 Accuracy
32	34.0%
64	38.8%
128	41.0%
256	40.1%

结论：128维是最优选择，性能在128维达到峰值。

训练数据量：

数据比例	Accuracy
0.1%	3.9%
1%	10.7%
10%	23.1%
30%	31.7%
100%	41.0%

结论：性能随训练数据量增加而持续提升，说明方法具有良好的可扩展性。

半监督学习

使用不同比例的标注数据进行微调：

标注比例	Ours (ResNet)	Scratch (ResNet)	Split-Brain (AlexNet)
1%	48.0%	38.0%	35.0%
2%	57.0%	46.0%	42.0%
4%	63.0%	54.0%	50.0%
10%	70.0%	65.0%	62.0%
20%	75.0%	72.0%	70.0%

结论：在少样本场景下优势明显，1%标注数据时领先10%。

目标检测

在PASCAL VOC 2007上的检测性能：

方法	AlexNet	VGG16	ResNet-50
Supervised	56.8%	67.3%	76.2%
Ours	48.1%	60.5%	65.4%

结论：在检测任务上达到无监督方法的SOTA，且随网络加深性能提升。

代码实现

核心损失函数实现

import torch
import torch.nn as nn
import torch.nn.functional as F

class InstanceDiscriminationLoss(nn.Module):
    """实例判别损失（使用NCE近似）"""
    
    def __init__(self, memory_bank, temperature=0.07, m=4096, lambda_reg=10.0):
        super().__init__()
        self.memory_bank = memory_bank  # [n, dim] 所有实例的特征
        self.temperature = temperature
        self.m = m  # 负样本数量
        self.lambda_reg = lambda_reg  # 正则化系数
    
    def forward(self, features, indices, memory_bank_prev):
        """
        Args:
            features: [batch_size, dim] 当前batch的特征
            indices: [batch_size] 当前batch的实例索引
            memory_bank_prev: [batch_size, dim] Memory Bank中的特征（上一迭代）
        """
        batch_size = features.size(0)
        device = features.device
        
        # L2归一化
        features = F.normalize(features, p=2, dim=1)
        
        # 从Memory Bank获取正样本特征
        pos_features = memory_bank_prev  # [batch_size, dim]
        
        # 随机采样负样本
        neg_indices = torch.randint(0, len(self.memory_bank), (batch_size, self.m), device=device)
        neg_features = self.memory_bank[neg_indices]  # [batch_size, m, dim]
        
        # 计算相似度
        pos_sim = torch.sum(features * pos_features, dim=1, keepdim=True) / self.temperature  # [batch_size, 1]
        neg_sim = torch.bmm(
            features.unsqueeze(1),  # [batch_size, 1, dim]
            neg_features.transpose(1, 2)  # [batch_size, dim, m]
        ) / self.temperature  # [batch_size, 1, m]
        
        # 估计归一化常数（蒙特卡洛）
        Z_approx = (len(self.memory_bank) / self.m) * torch.sum(torch.exp(neg_sim), dim=2)  # [batch_size, 1]
        
        # 计算概率
        pos_prob = torch.exp(pos_sim) / (torch.exp(pos_sim) + self.m * (1.0 / len(self.memory_bank)) * Z_approx)
        
        # NCE损失
        nce_loss = -torch.mean(torch.log(pos_prob + 1e-8))
        
        # 近端正则化
        reg_loss = self.lambda_reg * torch.mean(torch.sum((features - memory_bank_prev) ** 2, dim=1))
        
        total_loss = nce_loss + reg_loss
        
        return total_loss, nce_loss, reg_loss

完整训练流程

import torch
import torch.optim as optim
from torch.utils.data import DataLoader

class InstanceDiscriminationTrainer:
    def __init__(self, model, memory_bank, dataset_size, temperature=0.07, m=4096):
        self.model = model
        self.memory_bank = memory_bank  # 初始化为随机单位向量
        self.temperature = temperature
        self.m = m
        
        # 初始化Memory Bank
        self.memory_bank.data = F.normalize(
            torch.randn(dataset_size, 128), p=2, dim=1
        )
    
    def train_epoch(self, dataloader, optimizer, criterion):
        self.model.train()
        total_loss = 0
        
        for batch_idx, (images, indices) in enumerate(dataloader):
            # 前向传播
            features = self.model(images)  # [batch_size, 128]
            
            # 从Memory Bank获取上一迭代的特征
            memory_bank_prev = self.memory_bank[indices].clone()
            
            # 计算损失
            loss, nce_loss, reg_loss = criterion(
                features, indices, memory_bank_prev
            )
            
            # 反向传播
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            # 更新Memory Bank（动量更新）
            with torch.no_grad():
                self.memory_bank[indices] = F.normalize(features, p=2, dim=1)
            
            total_loss += loss.item()
            
            if batch_idx % 100 == 0:
                print(f'Batch {batch_idx}, Loss: {loss.item():.4f}, '
                      f'NCE: {nce_loss.item():.4f}, Reg: {reg_loss.item():.4f}')
        
        return total_loss / len(dataloader)

k-NN分类器实现

def knn_classify(query_features, memory_bank, memory_labels, k=200, temperature=0.07):
    """
    使用k-NN对查询特征进行分类
    
    Args:
        query_features: [n_query, dim] 查询特征
        memory_bank: [n_memory, dim] Memory Bank中的特征
        memory_labels: [n_memory] Memory Bank中的标签
        k: 最近邻数量
        temperature: 温度参数
    """
    # 计算相似度矩阵
    similarity = torch.mm(
        F.normalize(query_features, p=2, dim=1),
        F.normalize(memory_bank, p=2, dim=1).t()
    )  # [n_query, n_memory]
    
    # 找到top-k最近邻
    _, topk_indices = torch.topk(similarity, k, dim=1)  # [n_query, k]
    topk_similarities = torch.gather(similarity, 1, topk_indices)  # [n_query, k]
    topk_labels = memory_labels[topk_indices]  # [n_query, k]
    
    # 加权投票
    weights = torch.exp(topk_similarities / temperature)  # [n_query, k]
    
    # 对每个类别求和权重
    num_classes = memory_labels.max().item() + 1
    class_weights = torch.zeros(query_features.size(0), num_classes, device=query_features.device)
    
    for c in range(num_classes):
        mask = (topk_labels == c)  # [n_query, k]
        class_weights[:, c] = (weights * mask.float()).sum(dim=1)
    
    # 预测类别
    predictions = class_weights.argmax(dim=1)
    
    return predictions

技术细节

Memory Bank更新策略

选项1：直接替换

1	memory_bank[indices] = features

选项2：动量更新

1	memory_bank[indices] = momentum * memory_bank[indices] + (1 - momentum) * features

选项3：仅在训练时更新

训练时：每次迭代更新
测试时：固定不变

温度参数选择

典型值：0.07（与SimCLR、MoCo相同）
调优范围：0.05 - 0.15
影响：控制softmax分布的尖锐程度

NCE负样本数量

最小值：$m = 1$（性能较差）
推荐值：$m = 4096$（性能接近完整softmax）
权衡：$m$ 越大，性能越好，但计算成本也越高

近端正则化系数

典型值：$\lambda = 10.0$
作用：稳定训练，加速收敛
调优：根据训练稳定性调整

优缺点分析

优点

概念简单：将无监督学习转化为实例分类问题
非参数化：特征直接作为"类别原型"，泛化能力强
存储高效：128维特征，1M图像仅需600MB
可扩展性好：性能随数据和网络深度提升
训练测试一致：都使用相同的度量空间

缺点

计算成本：需要大量负样本（NCE）
Memory Bank维护：需要存储所有实例的特征
更新延迟：Memory Bank更新有延迟，可能影响性能
对数据增强依赖：需要合理的数据增强策略

与后续工作的关系

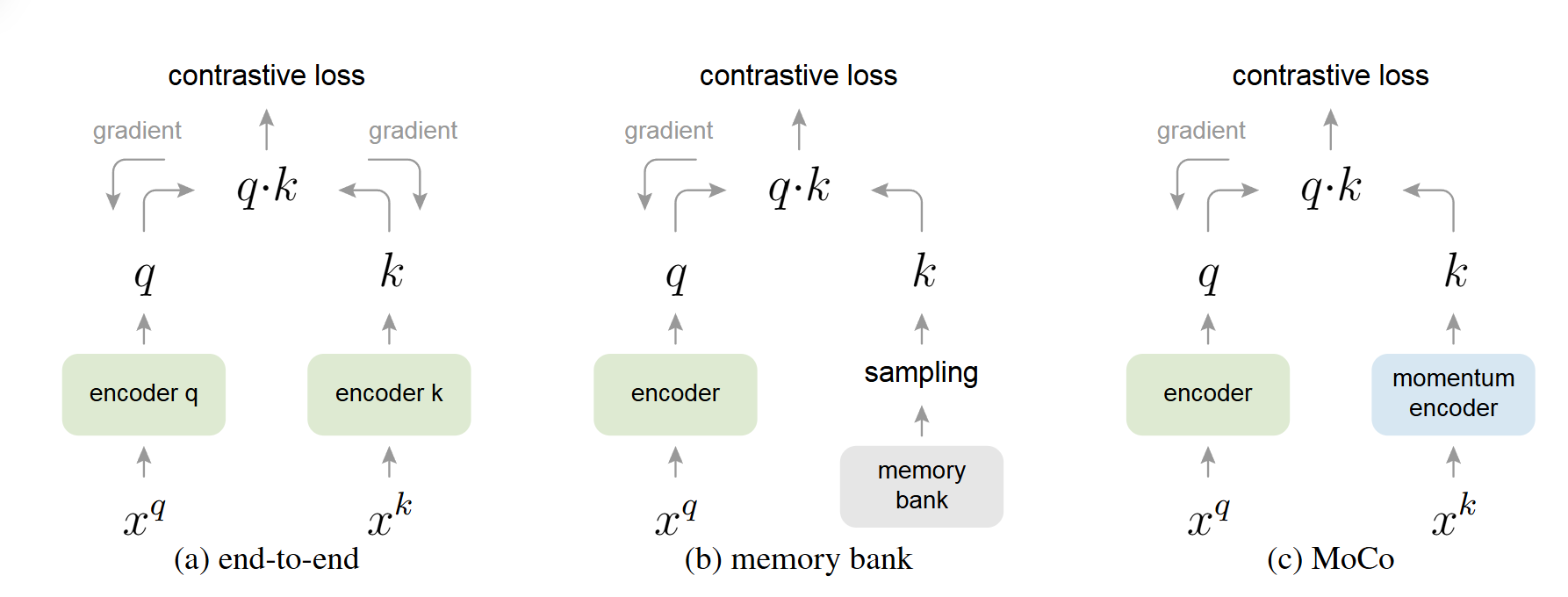
对MoCo的启发

Memory Bank → 队列：MoCo用队列替代Memory Bank
直接更新 → 动量更新：MoCo使用动量编码器
一致性保证：两者都关注特征的一致性

对SimCLR的启发

实例判别思想：SimCLR也使用实例判别
端到端训练：SimCLR去除了Memory Bank，使用大batch
数据增强重要性：SimCLR强调了数据增强的关键作用

对SupCon的启发

监督信号融入：SupCon将标签信息融入对比学习
同类样本作为正样本：SupCon扩展了正样本的定义

总结

实例判别学习通过将每个图像实例视为独立类别，使用非参数softmax和NCE来学习特征表示。其核心贡献包括：

非参数化设计：特征直接作为类别原型，泛化能力强
NCE近似：解决了大规模实例分类的计算问题
Memory Bank机制：高效存储和更新所有实例的特征
近端正则化：稳定训练过程

虽然后续的MoCo、SimCLR等方法在实现上更加优雅，但实例判别学习奠定了对比学习的基础思想，是这一领域的重要里程碑。

参考文献

Wu, Z., Xiong, Y., Yu, S. X., & Lin, D. (2018). Unsupervised feature learning via non-parametric instance discrimination. CVPR 2018. https://arxiv.org/pdf/1805.01978
Gutmann, M., & Hyvärinen, A. (2010). Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. AISTATS 2010.
He, K., et al. (2020). Momentum Contrast for Unsupervised Visual Representation Learning. CVPR 2020.
Chen, T., et al. (2020). A Simple Framework for Contrastive Learning of Visual Representations. ICML 2020.

思考题

为什么非参数softmax比参数化softmax更适合实例判别任务？
NCE如何将多类分类问题转化为二分类问题？为什么这样有效？
Memory Bank机制的优势和局限性是什么？与MoCo的队列机制有何区别？
近端正则化为什么能稳定训练？其背后的数学原理是什么？
实例判别学习与后续的MoCo、SimCLR在思想上有何联系和区别？
为什么k-NN分类器在测试时表现良好？这说明了什么？

思考题答案

1. 为什么非参数softmax比参数化softmax更适合实例判别任务？

参数化softmax的问题：

泛化能力弱：权重向量 $w_j$ 只对训练实例有效，无法应用到新实例
阻止直接比较：权重向量作为"类别原型"，阻止了实例特征间的直接比较
参数冗余：需要为每个实例存储一个权重向量，参数量大

非参数softmax的优势：

直接比较实例：特征向量 $v_j$ 直接作为"类别原型"，允许实例间的直接比较
泛化能力强：学习到的特征可以应用到任何新实例
参数高效：无需存储权重参数，只需存储特征
训练测试一致：训练和测试都使用相同的特征度量空间

实验验证：在CIFAR-10上，非参数方法比参数方法性能提升18%，证明了其优势。

2. NCE如何将多类分类问题转化为二分类问题？为什么这样有效？

转化过程：

原始问题：区分 $n$ 个类别（实例），需要计算所有类别的概率
NCE转化：将问题转化为"区分数据样本和噪声样本"的二分类问题
后验概率：
$$
h(i, v) = \frac{P_d(i\mid v)}{P_d(i\mid v) + m \cdot P_n(i)}
$$
其中 $P_d$ 是数据分布，$P_n$ 是噪声分布（均匀分布）

为什么有效：

计算效率：从 $O(n)$ 降低到 $O(1)$ 每个样本
近似质量：当负样本数量 $m$ 足够大时，近似质量接近完整softmax
理论基础：NCE有坚实的理论保证，是unnormalized模型的标准估计方法
实践验证：实验表明 $m=4096$ 时性能接近完整softmax

关键洞察：不需要计算所有类别的概率，只需要区分"是正样本"还是"是噪声样本"。

3. Memory Bank机制的优势和局限性是什么？与MoCo的队列机制有何区别？

Memory Bank的优势：

存储所有特征：可以访问训练集中所有实例的特征
计算高效：避免每次重新计算所有特征
历史信息：保留特征的历史状态

Memory Bank的局限性：

更新延迟：特征更新有延迟（使用上一迭代的特征）
内存需求：需要存储所有实例的特征
一致性挑战：特征可能因为编码器变化而变得不一致

与MoCo队列的区别：

特性	Memory Bank	MoCo队列
大小	所有训练实例	固定大小（如65536）
更新	直接替换	FIFO（先进先出）
一致性	可能不一致	通过动量编码器保证
存储	所有实例	仅最近batch的特征

MoCo的改进：

使用动量编码器保证Key的一致性
队列大小固定，内存可控
FIFO更新保证队列中的特征相对新鲜

4. 近端正则化为什么能稳定训练？其背后的数学原理是什么？

问题背景：

每个"类别"只有一个实例
每个epoch每个类别只访问一次
随机采样导致训练过程振荡严重

近端正则化的作用：

平滑性约束：鼓励当前特征 $v_i^{(t)}$ 与上一迭代特征 $v_i^{(t-1)}$ 接近
减少振荡：防止特征因为随机采样而剧烈变化
稳定梯度：使梯度更新更加平滑

数学原理：

近端正则化项：
$$
\lambda \big\lVert v_i^{(t)} - v_i^{(t-1)} \big\rVert_2^2
$$

这等价于在优化问题中加入平滑性约束：

当 $\lambda \to 0$：退化为原始损失
当 $\lambda \to \infty$：强制 $v_i^{(t)} = v_i^{(t-1)}$（不更新）

优化视角：
近端正则化是近端梯度方法的应用，用于优化非光滑或约束优化问题。在这里，它起到了稳定化的作用。

实验验证：图3显示，加入正则化后训练损失曲线更平滑，收敛更快。

5. 实例判别学习与后续的MoCo、SimCLR在思想上有何联系和区别？

共同思想：

实例判别：都将每个实例视为独立类别
对比学习：通过区分正负样本来学习特征
特征归一化：都使用L2归一化
温度参数：都使用温度缩放

主要区别：

特性	Instance Discrimination	MoCo	SimCLR
负样本来源	Memory Bank	队列	当前batch
特征更新	延迟更新	动量更新	实时更新
计算方式	NCE近似	完整softmax	完整softmax
batch size	小（256）	中等（1024）	大（≥4096）
实现复杂度	中等	较高	较低

演进关系：

Instance Discrimination：提出非参数softmax和Memory Bank
MoCo：改进Memory Bank为队列，引入动量编码器
SimCLR：去除Memory Bank，使用大batch和端到端训练

核心改进：

MoCo解决了Memory Bank的一致性问题
SimCLR简化了实现，但需要更多计算资源

6. 为什么k-NN分类器在测试时表现良好？这说明了什么？

k-NN表现良好的原因：

训练测试一致：训练和测试都使用相同的特征度量空间
非参数化设计：特征直接作为"类别原型"，适合k-NN
度量质量高：学习到的特征确实捕获了视觉相似性

实验证据：

在ImageNet上，k-NN准确率（46.5%）接近线性SVM（54.0%）
说明学习到的特征度量质量很高

深层含义：

训练目标有效：实例判别目标与语义分类目标一致
特征质量高：特征空间中的距离确实反映了视觉相似性
泛化能力强：学习到的表示可以泛化到新任务

对比其他方法：

Split-Brain：k-NN准确率（11.8%）远低于线性SVM（35.2%）
说明其学习到的特征度量质量较低

结论：k-NN的良好表现证明了实例判别学习的有效性，学习到的特征确实捕获了视觉相似性，而不仅仅是适合特定分类器的表示。

深入理解与实践思考

实例判别与语义判别的关系：虽然每个实例都被视作一个类别，但模型最终学习到的特征仍然会聚合出语义簇。这一现象说明视觉数据的结构性远强于我们赋予的标签结构。实际操作中可以通过t-SNE/UMAP观察到同类样本自然聚团。
Memory Bank vs. 队列：Memory Bank提供了全局视角，但需要处理“陈旧”特征的问题。后来MoCo中的动量编码器与固定长度队列，可以被视作对“特征一致性”与“可扩展性”的不同取舍。若业务中GPU显存紧张，可采用分片Memory Bank或结合近邻图的稀疏更新。
正则化的更广义含义：近端正则化不仅平滑了优化，还暗含“特征轨迹不能跳跃太远”的约束，相当于引入了一个时间维度的Lipschitz限制。这提醒我们，在设计自监督任务时，需要关注优化轨迹是否稳定。
评价指标的选择：k-NN性能高说明学到的度量空间质量好，但在工业场景往往还需关注召回、延迟等指标。实例判别学习天然适合构建向量检索服务（如图像去重、相似商品推荐）。
与现代方法的衔接：若希望复现最新SOTA，可在此框架上引入更强的编码器（ViT、ConvNeXt）、更丰富的数据增强（RandAugment、CutMix）以及更加稳定的优化器（AdamW + Cosine）。同时也可以尝试将SupCon的标签约束融入Memory Bank以获得更平滑的语义结构。

开放问题与研究方向

Memory更新策略：能否利用动量更新与自适应权重结合，既保持全局视野又不过度依赖旧特征？
负样本质量：如何更智能地采样“困难负样本”，避免CNN在易区分的负样本上浪费容量？
多模态扩展：能否直接在该框架中支持图像-文本或多模态实例判别，减少对比学习与跨模态模型之间的割裂？
理论解释：实例判别为何能自动恢复语义结构？是否存在可证明的聚类或流形假设支撑？
增量学习：面对不断新增的数据集，如何无缝扩展Memory Bank并避免遗忘？