深度学习损失函数：从 MSE 到 Focal Loss

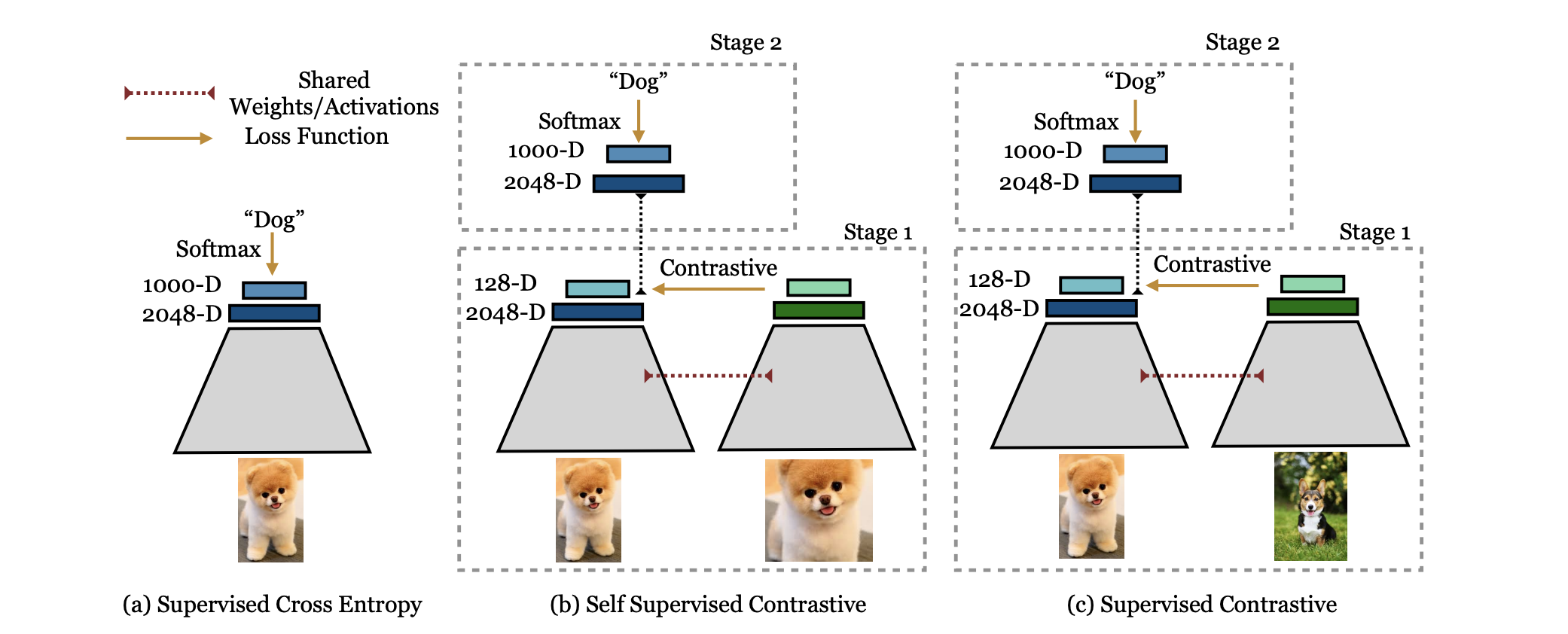
在深度学习中，损失函数 (Loss Function) 是连接模型预测与真实标签的桥梁，它定义了模型的优化目标。选择合适的损失函数往往能起到事半功倍的效果。本文将对深度学习中常见的损失函数进行梳理，从基础的回归/分类到进阶的难例挖掘和度量学习。

1. 回归任务 (Regression)

回归任务的目标是预测连续值。

1.1 MSE (L2 Loss)

均方误差 (Mean Squared Error)：
$$ L = (y - \hat{y})^2 $$

特点：收敛快，但对异常值 (Outliers) 非常敏感（因为误差被平方放大了）。

1.2 MAE (L1 Loss)

平均绝对误差 (Mean Absolute Error)：
$$ L = |y - \hat{y}| $$

特点：对异常值鲁棒，但在 0 点处不可导，梯度恒定可能导致收敛困难。

1.3 Smooth L1 Loss

结合了 L1 和 L2 的优点：

在误差较小时（$|x| < 1$）使用 L2（平滑，可导）。
在误差较大时（$|x| \ge 1$）使用 L1（梯度恒定，防止梯度爆炸）。
应用：Faster R-CNN 的边界框回归。

2. 分类任务 (Classification)

2.1 Cross Entropy (CE)

交叉熵损失是分类任务的标准配置：
$$ CE = - \sum y \log(p) $$

本质：衡量两个概率分布的距离（KL 散度）。
局限：对噪声标签敏感，且容易导致模型过度自信 (Over-confidence)。

2.2 Label Smoothing

为了解决 CE 的过度自信，Label Smoothing 将 One-hot 标签软化：
$$ y_{new} = (1 - \epsilon) y + \epsilon / K $$

作用：防止模型在训练集上过拟合，提升泛化能力。

3. 进阶：解决不平衡与难例

当数据存在严重的类别不平衡或大量简单负样本时，标准 CE 往往失效。

3.1 Focal Loss

最初用于目标检测 (RetinaNet)，旨在解决 One-stage 检测器中极端的正负样本失衡。

公式：$FL(p_t) = -\alpha_t (1 - p_t)^\gamma \log(p_t)$
核心机制：
- $\gamma$ (Focusing Parameter)：降低易分样本（$p_t \approx 1$）的权重，迫使模型关注难分样本。
- $\alpha$ (Balancing Parameter)：平衡正负样本比例。
价值：不仅用于检测，在长尾分类任务中也非常有效。

# Focal Loss PyTorch 实现
class FocalLoss(nn.Module):
    def __init__(self, alpha=1, gamma=2):
        super().__init__()
        self.alpha = alpha
        self.gamma = gamma
        
    def forward(self, inputs, targets):
        ce_loss = F.cross_entropy(inputs, targets, reduction='none')
        pt = torch.exp(-ce_loss)
        focal_loss = self.alpha * (1 - pt) ** self.gamma * ce_loss
        return focal_loss.mean()