Agentic RL：从 PG 到 TRPO 到 PPO-Clip（推导与代码对齐）

这篇文章面向“RL 基础薄弱但想快速读懂 PPO/Agentic RL 训练代码”的读者，目标是把下面三件事讲清楚，并且和你能跑起来的代码一一对应：

PG loss 到底是什么：它不是“监督学习意义上的 loss”，而是为了拿到正确梯度构造的 surrogate（代理目标）。
TRPO 想解决什么：为什么要用 KL trust region 限制策略更新幅度。
PPO-clip 为什么长这样：clip 不是拍脑袋，而是在做一个“好实现”的 trust region 近似。

系列导航：

Agentic RL：系列导航（PG Loss、TRPO、PPO-Clip）

配套资料来自 B 站视频与仓库（建议你边看边对照）：

视频 02：[Agentic RL] 02 策略梯度基础，从 PG 到 TRPO 到 PPO-Clip 核心公式简单推导
- https://www.bilibili.com/video/BV12NHJzTEoP/
视频 03：[Agentic RL] 03 策略梯度补充，GRPO loss 分析，优势标准化，On Policy
- https://www.bilibili.com/video/BV18hsFzbEKJ/
代码/笔记仓库：
- GitHub：wdkns/modern_genai_bilibili
- 核心 notebook：
  - agentic_rl/deep_RL/pg/from_pg_to_ppo-clip.ipynb（视频 02：推导主线）
  - agentic_rl/deep_RL/pg/policy_gradient.ipynb（视频 03：GRPO loss / 优势标准化 / On-policy + PPO case study）
- 一个“玩具 LLM-RL 对齐”脚本（REINFORCE + KL penalty）：
  - agentic_rl/deep_RL/scripts/reinforce_align.py

如果你更关心 PPO 训练工程里的 Dual-clip / Entropy / KL / Loss 聚合，建议先读我上一篇（组件解析更偏工程视角）：

Agentic RL：PG Loss 组件详解（PPO-clip / Dual-Clip / Entropy / KL / 聚合）

如果你希望把“推导”快速落到“训练调参/日志诊断”，建议你也顺带读：

Agentic RL：veRL（verl）训练参数理解（PPO & GRPO、Batch Size、KL & Entropy）

0. 先校正一个直觉：PG loss 不是“性能指标”，reward curve 才更像

监督学习里，你最小化的是一个“固定数据分布上的静态目标”。

而 RL（尤其 on-policy 的 PPO/GRPO）里，你每一轮采样的数据分布都在变：

第 $k$ 次更新，用的是由 $\pi_{\theta_k}$ 采样得到的数据分布 $\mathcal{D}_k$；
第 $k+1$ 次更新，用的是 $\pi_{\theta_{k+1}}$ 采样得到的 $\mathcal{D}_{k+1}$；

所以你日志里的 policy_loss 横向并不总可比，它更像“当前这一步的更新信号强弱”，而不是“模型变好了多少”。

在 LLM-RL / Agentic RL 里更是如此：你真正关心的通常是任务指标（成功率、RM reward、事实一致性、引用覆盖、成本等），它们才是你要看的 reward curve。

0.1 为什么 RL 的 loss curve 常常“越训越大/不单调”

在很多 LLM-RL/GRPO/PPO 的实现里，你看到的目标大致可以写成“策略项 + KL 正则”的形式（这里用 PPO-clip 举例）：

$$\mathcal{L}_k(\theta) = - \mathbb{E}_{(x,y) \sim \mathcal{D}_k} \left[ \min \left( r_\theta A, \text{clip}(r_\theta, 1 - \epsilon, 1 + \epsilon) A \right) \right] + \beta \cdot \mathbb{E}_{x \sim \mathcal{D}_k} \left[ \text{KL}(\pi_\theta(\cdot|x)|\pi_{\text{ref}}(\cdot|x)) \right]$$

关键点是：第 $k$ 轮和第 $k+1$ 轮的期望分布 $\mathcal{D}k$、$\mathcal{D}{k+1}$ 不是同一个，因为它们来自不同的策略采样。所以你画出来的 “loss curve” 很可能是在比较 “apple/orange/potato”，横向可比性天然很差。

更可操作的结论：

reward curve/任务指标优先于 loss curve。
loss 组件里更值得看的通常是：KL、clip fraction、entropy、adv/std 等“稳定性指标”。

0.2 这篇文章的“工程结论”清单（不看推导也能用）

如果你读完这篇只记住几条“能用来调参/读日志”的结论，我希望是这些：

PG/PPO 的 policy loss 是 surrogate，不是性能指标：跨 iteration 横向比较往往没意义，优先看 reward/成功率/任务指标。
PPO 的关键中间量就是 ratio：r = exp(logp_new - logp_old)。一旦你做多 epoch 更新或复用数据，它就会从 1 开始漂移。
PPO-clip 的目的不是“让 loss 变小”：而是让“有利方向的过度更新”被截平，避免一步跨太大导致崩。
TRPO/PPO 的约束本质是“更新别太猛”：工程上你通常用 approx_kl / clip_fraction / entropy 这种可观测量去闭环，而不是盯着一个理论上的 $\delta$。
在 LLM-RL 里，聚合方式改变数值尺度：token-level vs seq-level，sum vs mean，会直接改变“你以为的学习率/系数大小”。先把聚合讲清楚再谈超参区间。
多 epoch = 轻度 off-policy：PPO 常被叫 on-policy，但“rollout 很贵所以复用数据”会把你推向 off-policy drift；它不是原罪，但必须用 KL/clipfrac 监控。

（如果你想要一个“看到某个现象该动哪个旋钮”的表格版诊断，直接看 veRL 那篇的 调参诊断表。）

1. 我们到底在优化什么：轨迹期望回报 $J(\theta)$

在策略梯度（Policy Gradient）视角下，我们用参数 $\theta$ 的策略 $\pi_\theta(a|s)$ 与环境交互，产生轨迹（trajectory）：

$$\tau = (s_0, a_0, r_0, s_1, a_1, r_1, \ldots)$$

典型的目标是最大化期望折扣回报：

$$J(\theta) = \mathbb{E}_{\tau \sim \pi_\theta}\left[\sum_{t=0}^{T}\gamma^t r_t\right]$$

注意：$\tau$ 的分布是由 $\pi_\theta$ 决定的，这意味着你不是在对一个固定数据集做最优化，而是在对“会随着参数变化的采样分布”做最优化。

2. 为什么会出现 `log π`：log-trick（score function estimator）

你想对 $J(\theta)$ 求梯度，困难在于：期望是对一个依赖 $\theta$ 的分布取的。

关键技巧是：

$$\nabla_\theta \mathbb{E}_{x\sim p_\theta}[f(x)] =\mathbb{E}_{x\sim p_\theta}\big[f(x)\nabla_\theta\log p_\theta(x)\big]$$

把 $x$ 换成轨迹 $\tau$，并利用“环境转移不依赖 $\theta$（只依赖策略）”，可以推到经典的 REINFORCE / PG 形式：

$$\nabla_{\theta} J(\theta) = \mathbb{E}\left[\sum_t G_t \nabla_{\theta} \log \pi_{\theta}(a_t|s_t)\right]$$

其中 $G_t$ 是 return-to-go：

$$G_t = \sum_{k=t}^{T-1} \gamma^{k-t} r_k$$

这回答了你问的：

PG loss 里的 log π 从哪里来的？

它来自对分布求导时必须使用的 log-trick，否则你很难用采样/蒙特卡洛得到无偏梯度估计。

3. Advantage（baseline）：为什么从 $G_t$ 变成 $A_t$

REINFORCE 的梯度估计方差很大。一个经典做法是减去 baseline $b(s_t)$，不改变期望梯度，但显著降低方差：

$$A_t \doteq G_t - b(s_t)$$

直觉上，优势函数把“绝对分数”变成“相对平均水平的超额收益”：

$A_t > 0$：这步动作比平均水平好，应该提高它出现的概率；
$A_t < 0$：这步动作比平均水平差，应该降低它出现的概率。

在实现里，常见 baseline 就是 value function $V(s_t)$（Actor-Critic 体系），于是：

$$A_t \approx Q(s_t,a_t) - V(s_t)$$

3.1 折扣回报与 baseline 的直觉

折扣（discount）回答的是：离奖励越远的动作，对最终回报“负责得越少”。

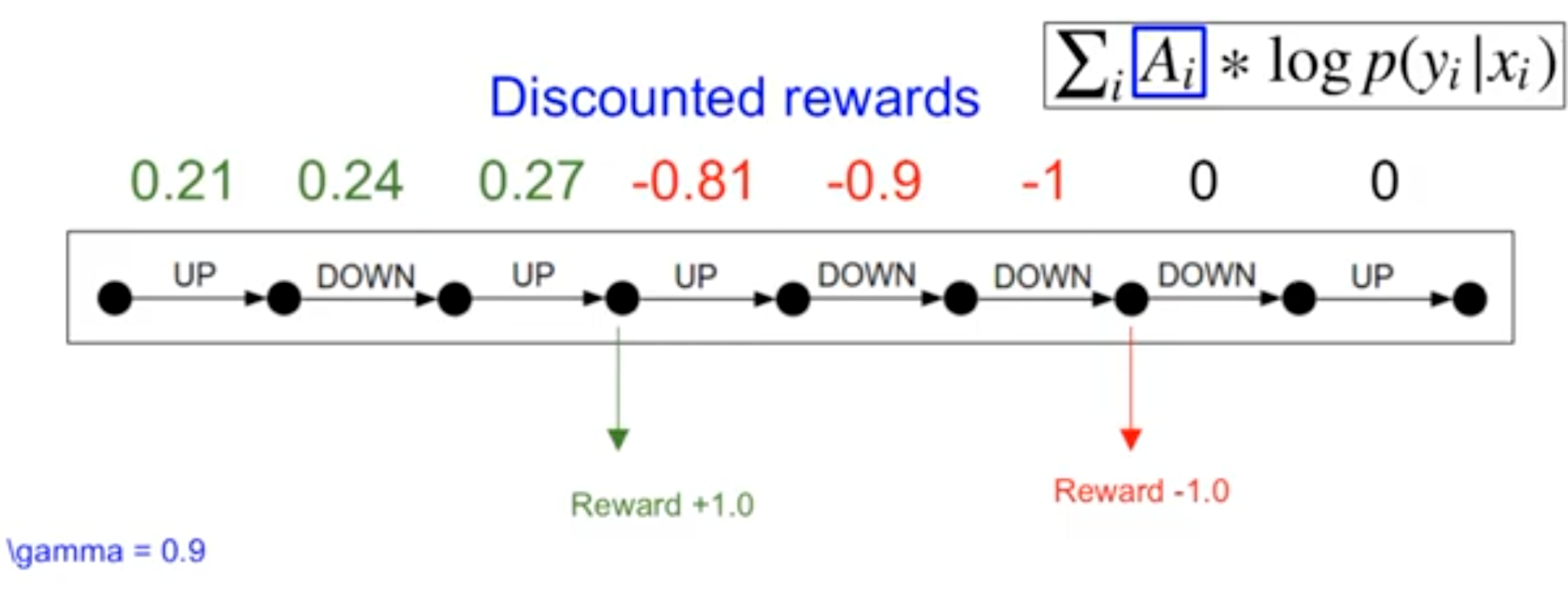
discounted-rewards

baseline 的直觉则是：把“绝对分数”变成“相对平均水平的超额收益”。哪怕你一直在输（return 是负数），也可能出现“比平均水平输得少”的一局，这局的 advantage 仍然是正的，策略依然应该提高那局里动作的概率。

4. PG loss 是什么：为了自动微分构造的 surrogate loss

深度学习框架默认做的是“最小化 loss”，所以我们把“最大化 $J$”改写成一个等价梯度方向的 surrogate loss：

$$\mathcal{L}_{PG}(\theta) = -\mathbb{E}\left[\sum_t A_t \log \pi_\theta(a_t|s_t)\right]$$

实现里你要记住一句话：

采样出来的 ${s_t,a_t,A_t}$ 当常数（stop-grad），让梯度只通过 $\log \pi_\theta$ 回传。

这也是为什么很多框架会对 advantages / old_logprobs 做 detach()。

4.1 PG vs Supervised Learning：为什么 PG loss 看起来像“加权交叉熵”

一个非常好用的对比（来自 Karpathy 的 RL 笔记）：

监督学习（交叉熵）最大化对数似然：$\sum_i \log p(y_i|x_i)$
- $y_i$ 是固定的 ground-truth label，数据集是静态的。
策略梯度（PG）最大化“带权重的对数似然”：$\sum_i A_i \log p(y_i|x_i)$
- 但这里没有 label，$y_i$ 是你从当前策略里采样出来的 action（token/动作），$A_i$ 是 credit assignment（优势/回报信号）。

所以你可以把 PG loss 视作一种“自采样数据上的加权 MLE”，权重就是 advantage。

5. 为什么 PPO 公式里看起来“没有 log”：重要性采样 ratio 来了

现实训练里，采样很贵。你通常会：

用旧策略 $\pi_{old}$ rollout 一批数据（轨迹/response）；
在同一批数据上做多次更新（多 epoch）。

这意味着你在优化新策略 $\pi_\theta$ 时，数据分布却来自 $\pi_{old}$。于是引入 重要性采样比率：

$$r_t(\theta) \doteq \frac{\pi_\theta(a_t|s_t)}{\pi_{old}(a_t|s_t)}$$

于是 CPI/TRPO 常写的 surrogate objective 是：

$$L_{CPI}(\theta) = \mathbb{E}_{\pi_{old}}[r_t(\theta)A_t]$$

5.1 LLM-RL 的一个实现关键：token-level ratio 与 seq-level ratio

在 LLM-RL 里，$a_t$ 是 token，$s_t$ 是“prompt + 已生成前缀”。因此 ratio 默认是 token-level：

$$r_t=\exp(\log\pi_\theta(a_t|s_t)-\log\pi_{old}(a_t|s_t))$$

如果你试图构造“整段输出”的序列级 ratio，那么它会变成连乘（对数空间是累加）：

$$r_{\text{seq}}=\prod_t r_t=\exp\left(\sum_t (\log\pi_\theta-\log\pi_{old})\right)$$

序列级 ratio 在长序列上数值会非常极端（爆炸/下溢），也会让优化目标对“长度”异常敏感。所以你会看到大多数工程实现（verl/openrlhf/trl 等）更倾向于：

用 token-level ratio 做 surrogate；
再用某种聚合（token mean / seq mean / group mean）把它变成一个标量 loss。

这也是为什么我一直强调：你看到的每一个 loss/KL/entropy 数值，都必须问清楚它是在哪个维度聚合出来的。

一个很关键的结论（也是“从 PG 到 TRPO 到 PPO”的桥）：

在 $\theta=\theta_{old}$ 附近，$L_{CPI}$ 的一阶梯度方向与 vanilla PG 一致。

这也解释了“PPO 公式为什么看起来没有 log”：

你在公式里看到的是 $r_tA_t$；
但代码里你仍然在算 r = exp(logp_new - logp_old)；
log 并没有消失，只是被你藏进 ratio 的计算里了。

6. TRPO：用 KL trust region 明确约束“更新别太猛”

仅最大化 $L_{CPI}$ 仍可能出现“策略一步跨太大导致性能崩”的问题。TRPO 的做法是加一个 trust region 约束：

$$\max_\theta\ \mathbb{E}_{\pi_{old}}[r_t(\theta)A_t] \quad \text{s.t.}\quad \mathbb{E}_{\pi_{old}}[KL(\pi_\theta|\pi_{old})] \le \delta$$

直觉：在“以旧策略为中心”的 KL 球里找一个最好的更新。

难点：这个约束优化更接近二阶优化（共轭梯度等），不太容易直接放进你熟悉的 mini-batch SGD 训练循环里。

6.1 方向别搞错：训练里你监控的 KL 往往不是你写在论文里的 KL

TRPO 的约束形式写成 $KL(\pi_\theta|\pi_{old})$ 还是 $KL(\pi_{old}|\pi_\theta)$，在理论推导里可以通过近似互相转换（小步近似下它们都接近同一个二次型）。但在工程里你通常监控的是一种 采样估计，它的方向往往是：

$$\text{approx_kl}(\pi_{old}|\pi_\theta)\approx \mathbb{E}_{a\sim\pi_{old}}[\log\pi_{old}(a|s)-\log\pi_\theta(a|s)]$$

它和 full-distribution 的 KL 不等价，只是“足够便宜且能反映漂移幅度”的 proxy。你做调参时的要点不是“哪一个更正确”，而是：

明确你日志里打印的 KL 估计到底是哪一种；
用同一种定义做横向对比和阈值判断；
结合 clip_fraction/entropy/reward 一起看，别只盯 KL。

7. PPO-clip：用 clip 做一个“好实现”的 TRPO 近似

PPO-clip 用一个工程上非常好实现的方式近似 trust region：

$$L_{CLIP}(\theta)=\mathbb{E}\left[\min\left(r_t(\theta)A_t,\ \text{clip}(r_t(\theta),1-\epsilon,1+\epsilon)\cdot A_t\right)\right]$$

你可以把它理解成：

$r_t$ 代表新旧策略概率变化倍率；
clip 把倍率限制在 $[1-\epsilon, 1+\epsilon]$；
min 让目标函数在“过度乐观”的那一侧被截平，从而更稳。

7.1 最重要的 case-by-case 结论（建议背下来）

$A_t>0$（好动作）
- 若 $r_t > 1+\epsilon$：上涨太猛，会被 clip 截平（梯度被压住）。
$A_t<0$（坏动作）
- 若 $r_t < 1-\epsilon$：下降太猛，会被 clip 截平（梯度被压住）。

一句话总结：

PPO-clip 主要限制“朝着对优势有利的方向”更新过头。

7.2 PPO-clip 的本质取舍：引入偏差换稳定性（不是免费的午餐）

clip 的效果可以理解成一个经典的 bias-variance tradeoff：

不 clip：目标更接近“真实的”重要性采样形式，但 ratio 一旦变大，方差会爆，训练很容易崩。
clip：对“过大更新”的样本把目标截平，显著降低方差与训练崩溃概率，但代价是引入偏差（你不再严格优化原目标）。

所以你在日志里看到 clip_fraction 很高时，不要只想着“更稳了”，而要问：

是不是我更新太激进（LR/epoch/batch/adv scale）导致大量样本触发剪裁，学习实际上被卡住？
是不是 reward 设计在诱导策略做极端动作，从而把 ratio 推爆？

这也是为什么 PPO 的“好用”来自一个非常工程化的前提：你得把更新幅度控制在一个合理范围里，让 clip 只在“救命”时生效，而不是常态。

8. PPO loss 为什么经常在 0 附近震荡：一个极简 case study

policy_gradient.ipynb 里用一个很实用的 toy 函数把 PPO-clip 的 per-sample 项拆开看：

import numpy as np

def ppo_terms(A, r, eps=0.2):
    A = np.asarray(A, dtype=float)
    r = np.asarray(r, dtype=float)
    r_clip = np.clip(r, 1 - eps, 1 + eps)
    term_pg = r * A
    term_clip = np.minimum(term_pg, r_clip * A)
    return A, r, r_clip, term_pg, term_clip

它帮你快速建立这样一个判断：

当“正优势样本多对应到 $r\ge 1$、负优势样本多对应到 $r\le 1$、且很少触发不利剪裁分支”时，$L_{clip}$ 往往偏正（最小化形式就是偏负）。
反过来，当正优势样本概率被压低、负优势样本概率大涨且被按更差的一边记账时，目标会偏负。

如果你把 advantage 做了零均值/标准化，那么在纯 on-policy（$\pi_{old}=\pi_\theta$）时 ratios 都是 1，PPO 的 PG 项也会很自然地在 0 附近摆动，这并不奇怪。

8.1 优势标准化（whiten）会让 loss 更“接近 0”，但不等于没有梯度

实践里经常会对 advantage 做标准化（whiten）：

$$\tilde A_t=\frac{A_t-\mathbb E[A]}{\text{Std}(A)}, \quad L_{\text{pg}}=-\mathbb E[\tilde A_t\log\pi_\theta(a_t|s_t)]$$

当 $\mathbb E[\tilde A]=0$ 时，$L_{\text{pg}}$ 的数值可以写成协方差形式：

$$\mathbb{E}[\tilde{A} \log \pi] = \operatorname{Cov}(\tilde{A}, \log \pi) + \mathbb{E}[\tilde{A}] \mathbb{E}[\log \pi] = \operatorname{Cov}(\tilde{A}, \log \pi)$$

这带来一个很重要的观测口径：

loss 的正/负，更多反映的是“策略是否更偏好优势动作”的相关性，而不是“任务好坏的绝对标尺”。
看到 loss 接近 0，并不能推出 grad=0 或“没学到”，更常见的是“尺度被重新定标/中心化了”。

9.（视频 03）GRPO loss 怎么看：为什么 `loss=0` 不等于 `grad=0`

GRPO/Group-based 方法的核心训练形态是：每个 prompt 采样一组（group）输出，用组内相对分数构造 advantage（常见是中心化/标准化），再做一个 PPO-clip 风格的 surrogate + KL anchor。

一种常见的写法是：

$$\mathcal{J}_{GRPO}(\theta)= \frac{1}{G} \sum_{i=1}^G \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \min \left( r_{i,t}(\theta)\hat{A}_{i,t}, \text{clip}\left(r_{i,t}(\theta), 1-\varepsilon, 1+\varepsilon\right)\hat{A}_{i,t} \right) - \beta D_{KL}(\pi_\theta|\pi_{ref})$$

其中 $r_{i,t}$ 就是 token-level ratio：$r_{i,t}=\exp(\log\pi_\theta-\log\pi_{\theta_{old}})$。

为什么经常会看到 “loss≈0”？

如果你把奖励/优势做了组内中心化（mean=0），那么策略项在“数值均值”意义上很容易接近 0；
但梯度取决于相关性（协方差项），并不等价于 0。

所以看 GRPO 训练日志时，更稳的做法是把 policy_loss 当作“当前更新信号的一种投影”，而把 reward/成功率 + KL/clip/entropy 等稳定性指标当作主监控项。

10. 最小可复现代码：CartPole 的 REINFORCE（对应 notebook）

下面这个实现来自 policy_gradient.ipynb 的核心代码（做了轻微排版），它能帮助你把“公式里的每一项”对应到代码里的每一步：

import gymnasium as gym
import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Categorical
import numpy as np

LEARNING_RATE = 0.01
GAMMA = 0.99
NUM_EPISODES = 200
DEVICE = torch.device("cuda:3" if torch.cuda.is_available() else "cpu")

class Policy(nn.Module):
    def __init__(self, state_dim, action_dim):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(state_dim, 128),
            nn.ReLU(),
            nn.Linear(128, action_dim),
            nn.Softmax(dim=-1),
        )

    def forward(self, x):
        return self.net(x)

class ReinforceAgent:
    def __init__(self, state_dim, action_dim):
        self.policy = Policy(state_dim, action_dim).to(DEVICE)
        self.optim = optim.Adam(self.policy.parameters(), lr=LEARNING_RATE)
        self.saved_log_probs = []
        self.rewards = []

    def select_action(self, state):
        state = torch.from_numpy(state).float().unsqueeze(0).to(DEVICE)
        probs = self.policy(state)
        dist = Categorical(probs)
        action = dist.sample()
        self.saved_log_probs.append(dist.log_prob(action))
        return action.item()

    def finish_episode(self):
        # 1) 计算 return-to-go（折扣回报）
        R = 0.0
        returns = []
        for r in reversed(self.rewards):
            R = r + GAMMA * R
            returns.insert(0, R)
        returns = torch.tensor(returns, device=DEVICE)

        # 2) 标准化 returns（等价于一种简单 baseline/方差控制）
        returns = (returns - returns.mean()) / (returns.std() + 1e-6)

        # 3) 构造 PG loss：-log_prob * return（越好越提升概率）
        policy_loss = []
        for log_prob, Rt in zip(self.saved_log_probs, returns):
            policy_loss.append(-log_prob * Rt)
        loss = torch.cat(policy_loss).sum()

        # 4) 一次反传更新
        self.optim.zero_grad()
        loss.backward()
        self.optim.step()

        self.rewards.clear()
        self.saved_log_probs.clear()
        return float(loss.item())

env = gym.make("CartPole-v1")
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = ReinforceAgent(state_dim, action_dim)

episode_rewards, episode_losses = [], []
for i in range(NUM_EPISODES):
    state, _ = env.reset()
    ep_reward = 0.0
    for t in range(500):
        a = agent.select_action(state)
        state, r, done, _, _ = env.step(a)
        agent.rewards.append(r)
        ep_reward += r
        if done:
            break
    episode_losses.append(agent.finish_episode())
    episode_rewards.append(ep_reward)
    if i % 50 == 0:
        print(i, ep_reward, np.mean(episode_rewards[-50:]))

读这段代码时，你可以逐行对照公式：

saved_log_probs 就是 $\log \pi_\theta(a_t|s_t)$；
returns（标准化后）扮演了 $A_t$ 的角色；
loss = -log_prob * A 就是 policy gradient surrogate loss。

11. 从 CartPole 到 LLM-RL：一个 REINFORCE + KL penalty 的玩具对齐脚本

仓库里有个非常直观的脚本：deep_RL/scripts/reinforce_align.py。

它做的事情可以一句话概括：

用语言模型采样一段文本（相当于 rollout）
用某个 reward function 给这段文本打分
用 REINFORCE 形式更新模型，并加一个 对 reference model 的 KL 正则 防止漂移

代码结构上最关键的两行就是：

$$\mathcal{L} \approx -(\text{logprob}) \cdot (\text{reward}) ;+; \beta \cdot KL(\pi_\theta|\pi_{ref})$$

这也能帮助你理解为什么 LLM-RL 训练里会出现：

policy（PG）项
KL 项
以及“为什么看起来 loss 在每轮都变了”

注意：这是 toy demo，目的不是追求工程最优，而是帮助你建立“公式-代码”映射。

12. 下一步读什么：把推导接到 Agentic RL / GRPO / verl 工程

如果你是奔着 Agentic RL（比如 deep research agent）来的，我建议你按这个顺序继续看仓库：

代理目标与 on-policy/off-policy：agentic_rl/deep_RL/objective_代理loss.ipynb
PPO 从零实现（建立直觉，不一定真训练）：agentic_rl/deep_RL/ppo/ppo_from_scratch.ipynb
verl 的 objective 与 loss 聚合（你上一篇 PG loss 组件文章也讲了很多）：agentic_rl/verl/objectives/objectives_loss.ipynb、agentic_rl/verl/objectives/agg_loss.ipynb
任务侧（deep research / search agent）：agentic_rl/tasks/deepresearch.ipynb、agentic_rl/tasks/search-agent.ipynb

最后提醒一句：做 agentic RL 不一定先从“微调 LLM”开始。很多深研究任务更有效的路径是：

先把评测闭环（reward/metrics）做扎实；
再决定训练的是“LLM 本体”还是“agent 决策层”（工具调用/检索/规划策略）。